题目内容
设等比数列{an}的前n项和为{an},若S3=3,S6=15,则S9=( )
| A、31 | B、32 | C、63 | D、64 |
考点:等比数列的前n项和
专题:等差数列与等比数列
分析:由等比数列的性质可得S3,S6-S3,S9-S6成等比数列,代值解方程即可.
解答:
解:由等比数列的性质可得S3,S6-S3,S9-S6成等比数列,
∴(S6-S3)2=S3(S9-S6),
代入数据可得(15-3)2=3(S9-15),
解得S9=63
故选:C
∴(S6-S3)2=S3(S9-S6),
代入数据可得(15-3)2=3(S9-15),
解得S9=63
故选:C
点评:本题考查等比数列的性质,得出S3,S6-S3,S9-S6成等比数列是解决问题的关键,属基础题.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
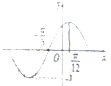 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0),|φ|≤
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0),|φ|≤| π |
| 2 |
A、f(x)=sin(2x+
| ||
B、f(x)=sin(2x-
| ||
C、f(x)=sin(4x+
| ||
D、f(x)=sin(4x-
|
算法程序如图所示,若输入-2,执行该程序后输出的y为( )


| A、3 | B、8 | C、16 | D、0 |
下列各组函数表示相等函数的是 ( )
A、f(x)=x+2与g(x)=
| |||||
| B、f(x)=(x-1)2与 g(x)=x-1 | |||||
C、f(x)=|x|与 g(x)=
| |||||
D、f(x)=
|
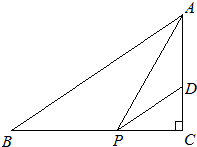 如图,直角△ABC中,∠C=90°,AB=2
如图,直角△ABC中,∠C=90°,AB=2