题目内容
已知f(α)=
.
(1)化简f(α);
(2)若角 A是△A BC的内角,且f(A)=
,求tan A-sin A的值.
sin(π-α)cos(-α)sin(
| ||
| cos(π+α)sin(-α) |
(1)化简f(α);
(2)若角 A是△A BC的内角,且f(A)=
| 3 |
| 5 |
考点:运用诱导公式化简求值
专题:计算题,三角函数的求值
分析:(1)运用诱导公式即可化简.
(2)由(1)知,cosA=
,由A是△ABC的内角,可求得sinA,tanA,即可得解.
(2)由(1)知,cosA=
| 3 |
| 5 |
解答:
解:(1)f(α)=
=cosα.…(5分)
(2)由(1)知,cosA=
,
∵A是△ABC的内角,
∴0≤A≤π,
∴sinA=
=
.…(7分)
∴tanA=
=
,
∴tanA-sinA=
-
=
. …(10分)
| sinαcosαcosα |
| (-cosα)(-sinα) |
(2)由(1)知,cosA=
| 3 |
| 5 |
∵A是△ABC的内角,
∴0≤A≤π,
∴sinA=
| 1-cos2A |
| 4 |
| 5 |
∴tanA=
| sinA |
| cosA |
| 4 |
| 3 |
∴tanA-sinA=
| 4 |
| 3 |
| 4 |
| 5 |
| 8 |
| 15 |
点评:本题主要考查了诱导公式,同角三角函数关系式的解法,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知等比数列{an}中,a1+a6=33,a2a5=32,公比q>1,则a3+a8=( )
| A、66 | B、132 |
| C、64 | D、128 |
下面不等式成立的是( )
| A、1.72.5>1.73 |
| B、log0.23<log0.25 |
| C、1.73.1<0.93.1 |
| D、log30.2<log0.20.3 |
图中阴影部分表示的集合是( )


| A、∁U(A∩B) |
| B、∁U(A∪B) |
| C、A∩(∁UB) |
| D、(∁UA)∩B |
复数(1-
)(1+i)=( )
| 1 |
| i |
| A、-2 | B、-2i | C、2 | D、2i |
已知集合A={x|1<x<5},B={x|x2-3x+2<0},则CAB=( )
| A、{x|2<x<5} |
| B、{x|2≤x<5} |
| C、{x|2≤x≤5} |
| D、∅ |
如图中O′A′B′C′为四边形OABC的斜二测直观图,则原平面图形OABC是( )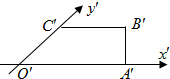
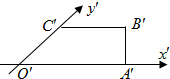
| A、直角梯形 |
| B、等腰梯形 |
| C、非直角且非等腰的梯形 |
| D、不可能是梯形 |