题目内容
14.用数学归纳法证明命题:1+2+3+…+n2=$\frac{{n}^{2}+{n}^{4}}{2}$时,则从n=k到n=k+1左边需增加的项数为( )| A. | 2n-1 | B. | 2n | C. | 2n+1 | D. | n2-n+1 |
分析 根据等式1+2+3+…+n2=$\frac{{n}^{2}+{n}^{4}}{2}$时,考虑n=k和n=k+1时,等式左边的项,再把n=k+1时等式的左端减去n=k时等式的左端,即可得到答案.
解答 解:当n=k时,等式左端=1+2++k2,
当n=k+1时,等式左端=1+2++k2+(k2+1)+(k2+2)+(k2+3)+…+(k+1)2,
所以增加的项数为:(k+1)2-(k2+1)+1=2k+1
即增加了2k+1项.
故选:C
点评 此题主要考查数学归纳法的问题,解答的关键是明白等式左边项的特点,再把n=k+1时等式的左端减去n=k时等式的左端.

练习册系列答案
相关题目
15.下列判断中正确的是( )
| A. | $f(x)={(\sqrt{x})^2}$是偶函数 | B. | $f(x)=\frac{{{x^2}-x}}{x-1}$是奇函数 | ||
| C. | $f(x)=\frac{{{2^x}+1}}{{{2^x}-1}}$是偶函数 | D. | $f(x)=\frac{{\sqrt{4-{x^2}}}}{|x-3|-3}$是奇函数 |
2.已知点P(-2,3),点Q(-6,-1),则直线PQ的倾斜角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 135° |
9.若集合P={x|2≤x<4},Q={x||x|>3},则P∩Q等于( )
| A. | {x|3<x<4} | B. | {x|-3<x<4} | C. | {x|2≤x<3} | D. | {x|2≤x≤3} |
6.抛物线y=-$\frac{1}{4}$x2的焦点与准线的距离为( )
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | 4 | D. | 2 |
 根据下列程序,当a的输入值为2,b的输入值为-2时,输出值为a、b,则ab=$-\frac{1}{2}$.
根据下列程序,当a的输入值为2,b的输入值为-2时,输出值为a、b,则ab=$-\frac{1}{2}$.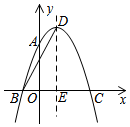 如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),抛物线的顶点为点D,对称轴与x轴交于点E,连结BD,则抛物线表达式:y=-x2+2x+3BD的长为2$\sqrt{5}$.
如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),抛物线的顶点为点D,对称轴与x轴交于点E,连结BD,则抛物线表达式:y=-x2+2x+3BD的长为2$\sqrt{5}$.