题目内容
19.已知函数f(x)=sin2xcosφ+cos2xsinφ(其中x∈R,0<φ<π).(1)求函数f(x)的最小正周期和值域;
(2)设若点($\frac{π}{6}$,$\frac{1}{2}$)在函数y=f(x+$\frac{π}{6}$)的图象上,求φ的值.
分析 (1)根据两角和与差的正弦函数对已知函数关系式进行化简得到f(x)=sin(2x+φ),所以结合正弦函数的性质来求最小正周期和值域;
(2)把( $\frac{π}{6}$,$\frac{1}{2}$)代入函数y=f(x+$\frac{π}{6}$),根据0<φ<π求φ的值.
解答 (1)解:∵f(x)=sin2xcosφ+cos2xsinφ=sin(2x+φ),即f(x)=sin(2x+φ),
∴函数f(x)的最小正周期为π,值域为[-1,1];
(2)解:∵函数y=f(x+$\frac{π}{6}$)=sin(2x+$\frac{π}{3}$+φ),
又点($\frac{π}{6}$,$\frac{1}{2}$)在函数y=f(x+$\frac{π}{6}$)的图象上,
∴sin($\frac{2π}{3}$+φ)=$\frac{1}{2}$.
∵0<φ<π,$\frac{2π}{3}$<$\frac{2π}{3}$+φ<$\frac{5π}{3}$,
∴$\frac{2π}{3}$+φ=$\frac{5π}{6}$,
解得:φ=$\frac{π}{6}$.
点评 本小题主要考查三角函数性质和三角函数的基本关系等知识,考查化归与转化的数学思想方法,以及运算求解能力.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
7.若一系列的函数解析式相同、值域相同,但定义域不同,则称这些函数为“同型异构”函数.那么函数解析式为y=-x2,x∈R,值域为{-1,-9}的“同型异构”函数有( )
| A. | 10个 | B. | 9个 | C. | 8个 | D. | 7个 |
4.“a>1”是“函数f(x)=(a2)x在定义域内是增函数”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.设集合A={x|(x+1)(2-x)>0},集合B={x|1<x<3},则A∪B=( )
| A. | (-1,3) | B. | (-1,1) | C. | (1,2) | D. | (2,3) |
8.某高校《统计初步》课程的教师随机调查了选修该课的学生的一些情况,具体数据如表1:为了判断主修统计专业是否与性别有关,根据表中数据,得K2的观察值为k=$\frac{{50×{{(13×20-10×7)}^2}}}{23×27×20×30}$≈4.844,所以判断主修统计专业与性别有关,那么这种判断出错的可能性不超过( )
| 表1 | 非统计专业 | 统计专业 |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
| P(K2≥k0) | 0.05 | 0.025 | 0.01 | 0.005 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 |
| A. | 5% | B. | 2.5% | C. | 1% | D. | 0.5% |
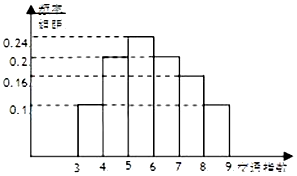 交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围为[0,10],分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如右图.
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围为[0,10],分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如右图.