题目内容
如图所示，正方体ABCD－A1B1C1D1的棱长为1，BD∩AC＝O，M是线段D1O上的动点，过点M作平面ACD1的垂线交平面A1B1C1D1于点N，则点N到点A距离的最小值为( )
A.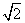
B.
C.
D．1
B
[解析] 连接B1D1，AN，则N在B1D1上．设MN＝x.在正方体ABCD－A1B1C1D1中可求得sin∠B1D1O＝
，则在Rt△D1MN中，D1N＝
＝x.又由正方体的性质知∠AD1N＝
，于是在△AD1N中，由余弦定理，得|AN|＝
所以当x＝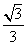
时，|AN|取得最小值，故选B.
练习册系列答案
口算能手系列答案
相关题目
在区间
上的最大值是 . . 
的最小值为________．
的正三角形，侧棱垂直于底面，且该三棱柱的外接球的表面积为12π，则该三棱柱的体积为________．
ln(1－x)的定义域是( )
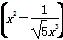5的展开式中的常数项为T，f(x)是以T为周期的偶函数，且当x∈[0,1]时，f(x)＝x，若在区间[－1,3]内，函数g(x)＝f(x)－kx－k有4个零点，则实数k的取值范围是________．