题目内容
6.向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$在正方形网络中的位置如图所示,若$\overrightarrow{c}$=λ$\overrightarrow{a}$+μ$\overrightarrow{b}$(λ,μ∈R),则$\frac{λ}{μ}$=( )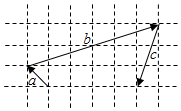
| A. | -8 | B. | -4 | C. | 4 | D. | 2 |
分析 设正方形的边长为1,则易知$\overrightarrow{c}$=(-1,-3),$\overrightarrow{a}$=(-1,1),$\overrightarrow{b}$=(6,2);从而可得(-1,-3)=λ(-1,1)+μ(6,2),从而求得.
解答 解:设正方形的边长为1,则易知
$\overrightarrow{c}$=(-1,-3),$\overrightarrow{a}$=(-1,1),$\overrightarrow{b}$=(6,2);
∵$\overrightarrow{c}$=λ$\overrightarrow{a}$+μ$\overrightarrow{b}$,
∴(-1,-3)=λ(-1,1)+μ(6,2),
解得,λ=-2,μ=-$\frac{1}{2}$;
故$\frac{λ}{μ}$=4;
故选:C.
点评 本题考查了平面向量的坐标表示的应用及学生的转化思想的应用.

练习册系列答案
相关题目
11.已知a>-2,若圆O1:x2+y2+2x-2ay-8a-15=0,圆O2:x2+y2+2ax-2ay+a2-4a-4=0恒有公共点,则a的取值范围为( )
| A. | (-2,-1]∪[3,+∞) | B. | $(-\frac{5}{3},-1)∪(3,+∞)$ | C. | $[-\frac{5}{3},-1]∪[3,+∞)$ | D. | (-2,-1)∪(3,+∞) |
18.已知z=2+i,(i是虚数单位),z的共轭复数是$\overline z$,则复数$\frac{\overline z}{i}$=( )
| A. | -1-2i | B. | 1-2i | C. | -1+2i | D. | 1+2i |
 设k≠0,若函数y1=(x-k)2+2k和y2=-(x+k)2-2k的图象与y轴依次交于A,B两点,函数y1,y2的图象的顶点分别为C,D.
设k≠0,若函数y1=(x-k)2+2k和y2=-(x+k)2-2k的图象与y轴依次交于A,B两点,函数y1,y2的图象的顶点分别为C,D.