题目内容
8．某校选定甲、乙、丙、丁、戊共5名教师去3个边远地区支教（每地区至少1人），其中甲和乙一定不同地，甲和丙必须同地，则不同的选派方案共有30种．分析 甲和丙同地，甲和乙不同地，所以有2、2、1和3、1、1两种分配方案，再根据计数原理计算结果．
解答 解：因为甲和丙同地，甲和乙不同地，所以有2、2、1和3、1、1两种分配方案，
①2、2、1方案：甲、丙为一组，从余下3人选出2人组成一组，然后排列：
共有：${C}_{3}^{2}$×${A}_{3}^{3}$=18种；
②3、1、1方案：在丁、戊中选出1人，与甲丙组成一组，然后排列：
共有：${C}_{2}^{1}$×${A}_{3}^{3}$=12种；
所以，选派方案共有18+12=30种．
点评 本题考查了分步技术原理，关键是分步，属于中档题．
练习册系列答案
相关题目
16．某几何体的三视图如图所示，则该几何体的体积为（ ）
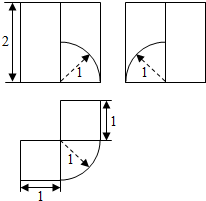
| A． | 6+$\frac{π}{8}$ | B． | 6+$\frac{π}{6}$ | C． | 4+$\frac{π}{8}$ | D． | 4+$\frac{π}{6}$ |
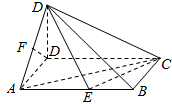如图，四边形ABCD为矩形，DD1⊥底面ABCD，AD=DD1=$\frac{1}{2}$AB，点F为AD1的中点．点E在棱AB上移动．
13．函数y=loga2（x2-2x-3），当x＜-1时为增函数，则a的取值范围是（ ）
| A． | a＞1 | B． | -1＜a＜1 | C． | -1＜a＜1且a≠0 | D． | a＞1或a＜-1 |