题目内容
已知PA垂直于平行四边形ABCD所在平面,若PC⊥BD,则平行四边形ABCD一定是 .
考点:直线与平面垂直的性质
专题:证明题,空间位置关系与距离
分析:根据题意,画出图形,利用线面平行的判定定理和性质定理,可知AC⊥BD,由对角线互相垂直的平行四边形是菱形.即可得出结论.
解答:
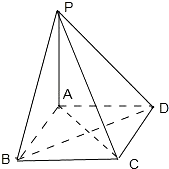 解:根据题意,画出图形如图,
解:根据题意,画出图形如图,
∵PA垂直平行四边形ABCD所在平面,
∴PA⊥BD,
又∵PC⊥BD,PA?平面ABCD,PC?平面ABCD,PA∩PC=P.
∴BD⊥平面PAC,
又∵AC?平面PAC,
∴AC⊥BD,
又ABCD是平行四边形,
∴平行四边形ABCD一定是菱形.
故答案为:菱形.
 解:根据题意,画出图形如图,
解:根据题意,画出图形如图,∵PA垂直平行四边形ABCD所在平面,
∴PA⊥BD,
又∵PC⊥BD,PA?平面ABCD,PC?平面ABCD,PA∩PC=P.
∴BD⊥平面PAC,
又∵AC?平面PAC,
∴AC⊥BD,
又ABCD是平行四边形,
∴平行四边形ABCD一定是菱形.
故答案为:菱形.
点评:此题考查学生的空间想象能力及线面垂直的判定与性质.由对角线互相垂直的平行四边形是菱形即可得出答案.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
函数f(x)=
的零点个数是( )
|
| A、0 | B、1 | C、2 | D、3 |
将全体正整数排成一个三角形数阵:
1
2 3
4 5 6
7 8 9 10
…
按照以上排列的规律,第8行从左向右的第5个数为( )
1
2 3
4 5 6
7 8 9 10
…
按照以上排列的规律,第8行从左向右的第5个数为( )
| A、30 | B、31 | C、32 | D、33 |
在数列{an}中,已知an=n2-n-50,则-8是该数列的( )
| A、第6项 | B、第7项 |
| C、第8项 | D、非任何一项 |
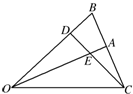 如图所示,已知△AOB中,点C与点B关于点A对称,
如图所示,已知△AOB中,点C与点B关于点A对称,