题目内容
11.在△ABC中,若BC=2,∠B=60°,△ABC的面积为3,则AC=$2\sqrt{4-\sqrt{3}}$.分析 利用三角形的面积求出BA,然后利用余弦定理求解即可.
解答 解:在△ABC中,若BC=2,∠B=60°,△ABC的面积为3,
可得3=$\frac{1}{2}×2×AB×\frac{\sqrt{3}}{2}$,AB=2$\sqrt{3}$,又BC=2,∠B=60°,
由余弦定理可得AC=$\sqrt{{BC}^{2}+{BA}^{2}-2BC•BAcosB}$=$\sqrt{4+12-2×2×2\sqrt{3}×\frac{1}{2}}$=2$\sqrt{4-\sqrt{3}}$.
故答案为:$2\sqrt{4-\sqrt{3}}$.
点评 本题考查余弦定理的应用,三角形的面积的求法,考查计算能力.

练习册系列答案
相关题目
20.目标函数z=x-y,在如图所示的可行域内(阴影部分且包括边界),使z取得最小值的点的坐标为( )


| A. | (1,1) | B. | (3,2) | C. | (5,2) | D. | (4,1) |
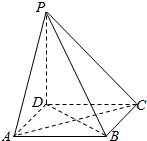 如图,四棱锥P-ABCD的各棱长都为a.
如图,四棱锥P-ABCD的各棱长都为a.