题目内容
6.将函数$y=sin(2x+\frac{π}{6})$的图象向左平移m(m>0)个单位长度,得到函数y=f(x)图象在区间$[-\frac{π}{12},\frac{5π}{12}]$上单调递减,则m的最小值为( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
分析 由题意利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性,可得 $\left\{\begin{array}{l}{2•(-\frac{π}{12})+2m+\frac{π}{6}≥2kπ+\frac{π}{2}}\\{2•\frac{5π}{12}+2m+\frac{π}{6}≤2kπ+\frac{3π}{2}}\end{array}\right.$,k∈Z,由此求得m的最小值.
解答 解:将函数$y=sin(2x+\frac{π}{6})$的图象向左平移m(m>0)个单位长度,可得y=sin(2x+2m+$\frac{π}{6}$)的图象;
再根据得到函数y=f(x)=sin(2x+2m+$\frac{π}{6}$)在区间$[-\frac{π}{12},\frac{5π}{12}]$上单调递减,
∴$\left\{\begin{array}{l}{2•(-\frac{π}{12})+2m+\frac{π}{6}≥2kπ+\frac{π}{2}}\\{2•\frac{5π}{12}+2m+\frac{π}{6}≤2kπ+\frac{3π}{2}}\end{array}\right.$,k∈Z,求得m=kπ+$\frac{π}{4}$,则m的最小值为$\frac{π}{4}$,
故选:C.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性,属于基础题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
16.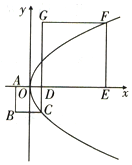 如图所示,正方形ABCD和正方形DEFG,原点O为AD的中点,抛物线y2=2px(p>0)经过C,F两点,则直线BE的斜率为( )
如图所示,正方形ABCD和正方形DEFG,原点O为AD的中点,抛物线y2=2px(p>0)经过C,F两点,则直线BE的斜率为( )
 如图所示,正方形ABCD和正方形DEFG,原点O为AD的中点,抛物线y2=2px(p>0)经过C,F两点,则直线BE的斜率为( )
如图所示,正方形ABCD和正方形DEFG,原点O为AD的中点,抛物线y2=2px(p>0)经过C,F两点,则直线BE的斜率为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $1-\frac{{\sqrt{2}}}{2}$ | C. | $2+\sqrt{2}$ | D. | $2-\sqrt{2}$ |
17.直线x-3y+3=0与圆(x-1)2+(y-3)2=10相交所得弦长为( )
| A. | $\sqrt{30}$ | B. | $\frac{5\sqrt{3}}{2}$ | C. | 4$\sqrt{2}$ | D. | 3$\sqrt{3}$ |
1. 如图,有一个水平放置的透明无盖的正三棱柱容器,其中侧棱长为8cm,底面边长为12cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时,测得水深为6cm,如果不计容器的厚度,则球的表面积为( )
如图,有一个水平放置的透明无盖的正三棱柱容器,其中侧棱长为8cm,底面边长为12cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时,测得水深为6cm,如果不计容器的厚度,则球的表面积为( )
 如图,有一个水平放置的透明无盖的正三棱柱容器,其中侧棱长为8cm,底面边长为12cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时,测得水深为6cm,如果不计容器的厚度,则球的表面积为( )
如图,有一个水平放置的透明无盖的正三棱柱容器,其中侧棱长为8cm,底面边长为12cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时,测得水深为6cm,如果不计容器的厚度,则球的表面积为( )| A. | 36πcm2 | B. | 64πcm2 | C. | 80πcm2 | D. | 100πcm2 |
11.如果函数y=f(x)在定义域内存在区间[a,b],使f(x)在[a,b]上的值域是[2a,2b],那么称f(x)为“倍增函数”.若函数f(x)=ln(ex+m)为“倍增函数”,则实数m的取值范围是( )
| A. | $(-\frac{1}{4},+∞)$ | B. | $(-\frac{1}{2},0)$ | C. | (-1,0) | D. | $(-\frac{1}{4},0)$ |
 已知函数f(x)=|3x-4|.
已知函数f(x)=|3x-4|.