题目内容
19.已知△ABC的顶点A(1,5),AB边上的中线CM所在直线方程为x-2y+5=0,AC边上的高BH所在直线方程为2x-y+5=0,求:(Ⅰ)顶点C的坐标;
(Ⅱ)直线BC的方程.
分析 (Ⅰ)设顶点C的坐标为( m,n),利用条件以及线段的中点公式、两条直线垂直的性质,求得m、n的值,可得点C的坐标.
(Ⅱ)设点B的坐标为(e,f),利用条件线段的中点公式,求得e、f的值,可得B的坐标,再利用式求得直线BC的方程.
解答 解:(Ⅰ)设顶点C的坐标为( m,n),则由点C在直线CM上,可得m-2n+5=0 ①.
再根据AC⊥BH,可得$\frac{n-5}{m-1}$•2=-1 ②,
由①②求得 $\left\{\begin{array}{l}{m=3}\\{n=4}\end{array}\right.$,∴C(3,4).
(Ⅱ)设点B的坐标为(e,f),则AB的中点($\frac{e+1}{2}$,$\frac{f+5}{2}$)在CM:x-2y+5=0上,
∴$\frac{e+1}{2}$-2•$\frac{f+5}{2}$+5=0,即e-2f-4=0 ③.
再根据点B的坐标为(e,f) 满足BH所在直线方程2x-y+5=0,可得2e-f+5=0 ④,
由③④求得$\left\{\begin{array}{l}{e=-\frac{14}{3}}\\{f=-\frac{13}{3}}\end{array}\right.$,∴B(-$\frac{14}{3}$,-$\frac{13}{3}$),由两点式求得直线BC的方程为$\frac{y-4}{-\frac{13}{3}-4}$=$\frac{x-3}{-\frac{14}{3}-3}$,
即 25x-23y+17=0.
点评 本题主要考查两条直线垂直的性质,线段的中点公式,用两点式求直线的方程,属于中档题.

练习册系列答案
相关题目
11.对于函数y=sin($\frac{13}{2}$π-x),下面说法中正确的是( )
| A. | 函数是周期为2π的偶函数 | B. | 函数是周期为π的偶函数 | ||
| C. | 函数是周期为2π的奇函数 | D. | 函数是周期为π的奇函数 |
8.阅读下面的程序框图,运行相应的程序,则输出的K和S的值分别为( )
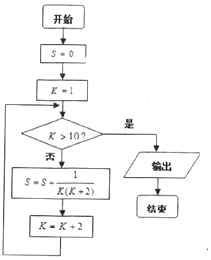

| A. | 9,$\frac{4}{9}$ | B. | 11,$\frac{5}{11}$ | C. | 11,$\frac{10}{11}$ | D. | 13,$\frac{12}{13}$ |
 ,其中A的各位数字中,a1=1,且ak(k=2,3,4,5)为0和1的概率分别是$\frac{1}{4}$和$\frac{3}{4}$.记ξ=a1+a2+a3+a4+a5,当程序运行一次时:
,其中A的各位数字中,a1=1,且ak(k=2,3,4,5)为0和1的概率分别是$\frac{1}{4}$和$\frac{3}{4}$.记ξ=a1+a2+a3+a4+a5,当程序运行一次时: 如图,在正方体ABCD-A'B'C'D'中,E为DD'的中点.
如图,在正方体ABCD-A'B'C'D'中,E为DD'的中点.