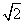题目内容
已知函数f(x)=-x2+2ax+1-a在0≤x≤1时有最大值2,求a的值.
当对称轴x=a<0时,如图1所示.
当x=0时,y有最大值,ymax=f(0)=1-a.
∴1-a=2,即a=-1,且满足a<0,∴a=-1.

图1 图2
当0≤a≤1时,如图2所示.即当x=a时,y有最大值,
ymax=f(a)=-a2+2a2+1-a=a2-a+1.

图3
∴a2-a+1=2,解得a= .
.
∵0≤a≤1,∴a= 舍去.
舍去.
当a>1,如图3所示.
由图可知,当x=1时y有最大值,
ymax=f(1)=2a-a=2,
∴a=2,且满足a>1,∴a=2.
综上可知,a的值为-1或2.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
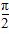 )=f(x-
)=f(x- ,则k+α=________.
,则k+α=________. ,则m的取值范围是( )
,则m的取值范围是( ) B.
B. 

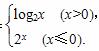 若f(a)=
若f(a)=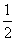 ,则实数a=( )
,则实数a=( )