题目内容

4．已知命题p：?x∈R，x-1＞lgx，命题q：?x≥0，x≥sinx，则（　　）
A．命题p∨q是假命题B．命题p∧q是真命题
C．命题p∨（￢q）是假命题D．命题p∧（￢q）是真命题

分析 分别判断出p，q的真假，从而判断出复合命题的真假即可．

解答 解：命题p：取x=1时，x-1≥lgx，成立，因此p是真命题．
命题q：令f（x）=x-sinx，f′（x）=1-cosx≥0，
f（x）在[0，+∞）递增，f（x）min=f（0）=0，
故命题q是真命题，
故p∧q是真命题，
故选：B．

点评 本题考查了复合命题的判断，考查三角函数以及对数函数问题，是一道基础题．

练习册系列答案
相关题目
14．已知数列{an}前n项和为Sn，首项为a1，且$\frac{1}{2}$，an，Sn成等差数列．
（1）求数列{an}的通项公式；
（2）数列{bn}满足bn=（log2a2n+1）×（log2a2n+3），求数列{$\frac{1}{{b}_{n}}$}的前n项和．
15．设a＞0，则${∫}_{-a}^{a}$$\frac{xdx}{1+cosx}$=（　　）
A．1B．0C．2aD．$\frac{3}{4}$a
12．已知|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1，它们的夹角为θ，且$\overrightarrow{a}$•$\overrightarrow{b}$=$-\frac{1}{2}$．
（1）求θ的值；
（2）求|3$\overrightarrow{a}$+5$\overrightarrow{b}$|；
（3）若（3$\overrightarrow{a}$+k$\overrightarrow{b}$）⊥（k$\overrightarrow{a}$-$\overrightarrow{b}$），求k的值．
19．$\frac{1}{1×3}$+$\frac{1}{2×4}$+$\frac{1}{3×5}$+…+$\frac{1}{8×10}$=（　　）
A．$\frac{9}{10}$B．$\frac{9}{20}$C．$\frac{29}{45}$D．$\frac{29}{90}$
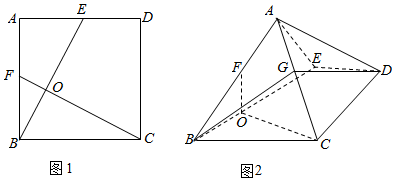9．已知函数y=sin（2x+φ），φ∈（0，$\frac{π}{2}$）经过点（$\frac{π}{6}$，1），则φ=$\frac{π}{6}$．
16．集合A={x|x+y=1}，B={（x，y）|x-y=1}，则A∩B=∅．
7．如图1已知正方形ABCD的边长为2，E，F分别为边AD、AB的中点，将△ABE沿BE折起，使平面ABE⊥平面BCDE，如图2，点G为AC的中点
（Ⅰ）求证：DG∥平面ABE；
（Ⅱ）求椎体G-ABE的体积．
8．过点P（3，1）的直线l与圆C：（x-2）2+（y-2）2=4相交于A，B两点，当弦AB的长取最小值时，直线l的倾斜角等于45°．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网