题目内容
16.设△ABC的内角A,B,C所对的边分别为a,b,c,已知$\frac{a+b}{sin(A+B)}$=$\frac{a-c}{sinA-sinB}$.(Ⅰ)求角B;
(Ⅱ)如果b=2,求△ABC面积的最大值.
分析 (Ⅰ)根据正弦定理和余弦定理即可求出B的大小;
(Ⅱ)当b=2时,由(1)的结论可得a2+c2-4=ac,利用基本不等式可求出ac≤4,再根据三角形的面积公式即可求出最大值.
解答 解:(Ⅰ)△ABC中,由正弦定理可得$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$,A+B=π-C,
∴$\frac{a+b}{sin(A+B)}$=$\frac{a-c}{sinA-sinB}$⇒$\frac{a+b}{c}$=$\frac{a-c}{a-b}$,
∴a2-b2=ac-c2,
∴a2+c2-b2=ac,
由余弦定理可得cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{ac}{2ac}$=$\frac{1}{2}$,
∵0<B<π,
∴B=$\frac{π}{3}$;
(Ⅱ)∵b=2,
∴a2+c2-4=ac,
∴2ac-4≤ac,
∴ac≤4,当且仅当a=c=2时取等号,
∴S△ABC=$\frac{1}{2}$acsinB=$\frac{\sqrt{3}}{4}$ac≤$\sqrt{3}$,
∴△ABC面积的最大值为$\sqrt{3}$.
点评 本题主要考查了正弦定理,余弦定理,基本不等式的应用,三角形面积公式的应用,属于中档题.

练习册系列答案
相关题目
6.直线l1:ax-y-3=0,x+by+c=0,则ab=-1是l1∥l2的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.两线段AB、CD不在同一平面内,如果AC=BD,AD=BC,则AB与CD( )
| A. | 垂直 | B. | 平行 | C. | 相交 | D. | 以上都不对 |
8.等比数列{an}满足a1=2,a1+a3=12,则a3+a5=( )
| A. | 24 | B. | 28 | C. | 60 | D. | 108 |
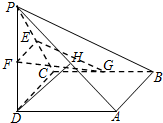 如图,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB,E,F,G,H分别为PC、PD、BC、PA的中点.
如图,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB,E,F,G,H分别为PC、PD、BC、PA的中点.