题目内容
20.已知sinαcosα=$\frac{1}{8}$,且α是第三象限角.求$\frac{{1-{{cos}^2}α}}{{cos(\frac{3π}{2}-α)+cosα}}$+$\frac{{sin(α-\frac{7π}{2})+sin(2017π-α)}}{{{{tan}^2}α-1}}$.
分析 利用同角三角函数的基本关系、诱导公式把要求的式子化为-(sinα+cosα),再根据sinαcosα=$\frac{1}{8}$,且α是第三象限角求得sinα+cosα的值,可得原式的值.
解答 解:原式=$\frac{{{{sin}^2}α}}{-sinα+cosα}+\frac{cosα+sinα}{{\frac{{{{sin}^2}α-{{cos}^2}α}}{{{{cos}^2}α}}}}$=$\frac{{-{{sin}^2}α}}{sinα-cosα}+\frac{{(cosα+sinα){{cos}^2}α}}{{{{sin}^2}α-{{cos}^2}α}}$=$\frac{{-{{sin}^2}α}}{sinα-cosα}+\frac{{{{cos}^2}α}}{sinα-cosα}$=$\frac{{{{cos}^2}α-{{sin}^2}α}}{sinα-cosα}=-(sinα+cosα)$,
∵$sinαcosα=\frac{1}{8}$,∴${(sinα+cosα)^2}=1+2sinαcosα=\frac{5}{4}$.
∵α是第三象限的角,
∴sinα<0,cosα<0,∴$sinα+cosα=-\frac{{\sqrt{5}}}{2}$,
∴原式=$\frac{{\sqrt{5}}}{2}$.
点评 本题主要考查同角三角函数的基本关系、诱导公式的应用,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
15.若实数m=${∫}_{1}^{e}$$\frac{1}{x}$dx,过点(-1,0)作曲线y=x2+x+m切线,其中一条切线方程是( )
| A. | 2x+y+2=0 | B. | 3x-y+3=0 | C. | x+y+1=0 | D. | x-y+1=0 |
9.已知直线l是曲线C1:y=x2与曲线C2:y=lnx,x∈(0,1)的一条公切线,若直线l与曲线C1的切点为P,则点P的横坐标t满足( )
| A. | 0<t<$\frac{1}{2}$ | B. | $\frac{1}{2}$<t<1 | C. | $\frac{\sqrt{2}}{2}$<t<$\sqrt{2}$ | D. | $\sqrt{2}$<t<$\sqrt{3}$ |
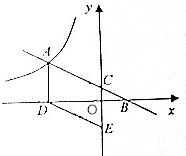 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E,已知四边形ADEC的面积为6.
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E,已知四边形ADEC的面积为6.