题目内容

5．函数y=x3-3x2+3的图象与函数y=$\frac{x-2}{x-1}$的图象的所有交点的纵坐标之和为（　　）
A．-2B．0C．2D．4

分析 画出图象，可知函数y=x3-3x2+3的图象与函数y=$\frac{x-2}{x-1}$的图象关于点（1，1）中心对称．即可得出．

解答 解：由于函数y=$\frac{x-2}{x-1}$=1-$\frac{1}{x-1}$，可知其定义域为{x|x≠1}，其两条渐近线方程分别为：x=1，y=1．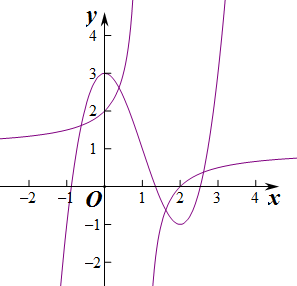

画出图象：可知：函数y=x3-3x2+3的图象与函数y=$\frac{x-2}{x-1}$的图象关于点（1，1）中心对称．
根据图象的对称性可得所有交点的纵坐标之和等于4．
故选：D．

点评 本题考查了利用函数的图象的对称性解决问题，考查了反比例函数的图象、三次函数的图象、图象的变换，考查了数形结合的思想方法，属于难题．

练习册系列答案
相关题目
15．已知函数f（x）=2$\sqrt{3}$sinx•cosx-2sin2x+1（x∈R）
（1）设函数g（x）=f（x+$\frac{φ}{2}$），φ∈（0，π），若g（x）为偶函数，求g（x）最大值及相应的x值的集合．
（2）将函数f（x）的图象向右平移$\frac{π}{4}$个单位，再将图象上各点的横坐标伸长到原来的2倍（纵坐标不变），得到函数y=h（x）的图象，若关于x的方程h（x）+k=0，在区间[0，π]上有实数解，求实数k的取值范围．
16．过点（0，-2）与抛物线y2=8x只有一个公共点的直线有（　　）
A．1条B．2条C．3条D．4条
13．奇函数y=f（x）在[1，2]上是增函数且有最大值5，则y=f（x）在[-2，1]上是（　　）
A．增函数且有最小值-5B．增函数且有最大值-5
C．减函数且有最小值-5D．减函数且有最大值-5
20．计算下列各式的值：
（1）sin$\frac{π}{8}$cos$\frac{π}{8}$；
（2）sin2$\frac{π}{8}$-$\frac{1}{2}$．
10．求下列各函数的导数．
（1）y=（3x2-4x）（2x+1）；
（2）y=x2sinx；
（3）y=$\frac{lnx}{{x}^{2}+1}$；
（4）y=（$\sqrt{x}$+1）（$\frac{1}{\sqrt{x}}$-1）．
17．若函数f（x）=$\frac{x+a}{2{x}^{2}-1}$，x∈（-∞，b）∪（b+2，+∞）是奇函数，则a+b=-1．
14．已知数列{an}中，a1=1，（n2+2n）an-n2an-1=0（n∈N*，n≥2），则an=$\frac{6}{（n+1）（n+2）}$．
20．已知sinαcosα=$\frac{1}{8}$，且α是第三象限角．
求$\frac{{1-{{cos}^2}α}}{{cos（\frac{3π}{2}-α）+cosα}}$+$\frac{{sin（α-\frac{7π}{2}）+sin（2017π-α）}}{{{{tan}^2}α-1}}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网