题目内容
3．
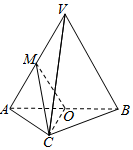如图，在三棱锥V-ABC中，平面VA B⊥平面 ABC，AC=BC，O，M分别为A B，VA的中点．（Ⅰ）求证：VB∥平面 M OC；
（Ⅱ）求证：平面MOC⊥平面VAB．
分析 （1）利用中位线定理可得MO∥VB，从而得出VB∥平面MOC；
（2）由三线合一可得OC⊥AB，由平面VAB⊥平面ABC可得OC⊥平面VAB，故而平面MOC⊥平面VAB．
解答 证明：（I）∵M，O分别为VA，AB的中点，
∴MO∥VB，又MO?面MOC，VB?面MOC，
∴VB∥面MOC．
（Ⅱ）∵AC=BC，O为AB的中点，
∴OC⊥AB．又∵平面VAB⊥平面ABC，平面VAB∩平面ABC=AB，OC?平面ABC，
∴OC⊥平面VAB．又∵OC?平面MOC，
∴平面MOC⊥平面VAB．
点评 本题考查了线面平行的判定，面面垂直的性质与判断，属于基础题．
练习册系列答案
相关题目
11．与圆（x+1）2+y2=1和圆（x-5）2+y2=9都相切的圆的圆心轨迹是（ ）
| A． | 椭圆和双曲线 | B． | 两条双曲线 | C． | 双曲线的两支 | D． | 双曲线的一支 |
18．数列1，3，7，15，31，…的一个通项公式为（ ）
| A． | an=2n-1 | B． | an=2n+1 | C． | ${a_n}={n^2}-1$ | D． | an=n2+1 |
15．在曲线y=x2（x≥0）上某一点A处作一切线使之与曲线以及x轴所围成的面积为$\frac{2}{3}$，则切点A的坐标为（ ）
| A． | （1，1） | B． | （2，4） | C． | （$\sqrt{2}$，2） | D． | （$\frac{1}{2}$，$\frac{1}{4}$） |
12．一个几何体的三视图如图所示，其中正视图是正三角形，则几何体的表面积为（ ）
| A． | $4（1+\sqrt{3}+\sqrt{7}）$ | B． | $4（\sqrt{3}+\sqrt{7}）$ | C． | $8（1+\sqrt{3}+\sqrt{7}）$ | D． | $8（\sqrt{3}+\sqrt{7}）$ |
13．已知命题p：?x∈R，x＞sinx，则p的否定形式为（ ）
| A． | ?x0∈R，x0＜sinx0 | B． | ?x0∈R，x0≤sinx0 | C． | ?x∈R，x≤sinx | D． | ?x∈R，x＜sinx |