题目内容
17．△ABC中，内角A、B、C对的边分别为a、b、c，如果△ABC的面积等于8，a=5，tanB=-$\frac{4}{3}$，那么$\frac{a+b+c}{sinA+sinB+sinC}$=$\frac{5\sqrt{65}}{4}$．分析 求出sinB，利用三角形的面积公式求出c的长度，进一步利用余弦定理求出b的长度，在应用正弦定理和等比性质求出结果．
解答 解：△ABC中，∵tanB=-$\frac{4}{3}$，∴sinB=$\frac{4}{5}$，cosB=-$\frac{3}{5}$．
又S=$\frac{1}{2}acsinB$=2c=8，∴c=4，
∴b=$\sqrt{{a}^{2}+{c}^{2}-2accosB}$=$\sqrt{65}$．
∴$\frac{a+b+c}{sinA+sinB+sinC}$=$\frac{b}{sinB}$=$\frac{5\sqrt{65}}{4}$．
故答案为：$\frac{5\sqrt{65}}{4}$．
点评 本题考查的知识点：三角形的面积公式，余弦定理和正弦定理的应用，等比性质的应用．
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
5．在△ABC中M是BC的中点，BC=8，AM=3，AM⊥BC，则$\overrightarrow{AB}$•$\overrightarrow{AC}$=（ ）
| A． | -7 | B． | -$\frac{7}{2}$ | C． | 0 | D． | 7 |
2．函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的最小正周期为π，且其图象经过点（$\frac{7π}{12}$，0），则函数f（x）在区间[0，$\frac{π}{2}$]上的最大值与最小值的和为（ ）
| A． | 1-$\frac{\sqrt{3}}{2}$ | B． | 0 | C． | $\frac{1}{2}$ | D． | 1+$\frac{\sqrt{3}}{2}$ |
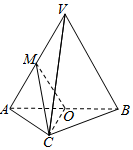如图，在三棱锥V-ABC中，平面VA B⊥平面 ABC，AC=BC，O，M分别为A B，VA的中点．