题目内容
15.在曲线y=x2(x≥0)上某一点A处作一切线使之与曲线以及x轴所围成的面积为$\frac{2}{3}$,则切点A的坐标为( )| A. | (1,1) | B. | (2,4) | C. | ($\sqrt{2}$,2) | D. | ($\frac{1}{2}$,$\frac{1}{4}$) |
分析 设A(m,m2),求出y=x2(x≥0)的导数,可得切线的斜率,求得切线的方程,运用定积分和三角形的面积公式可得,${∫}_{0}^{m}$x2dx-$\frac{1}{2}$m2•(m-$\frac{m}{2}$)=$\frac{2}{3}$,计算即可得到切点A的坐标.
解答 解:设A(m,m2),y=x2(x≥0)的导数为y′=2x,
可得切线的斜率为2m,
切线的方程为y-m2=2m(x-m),
令y=0,可得x=$\frac{m}{2}$,
由题意可得${∫}_{0}^{m}$x2dx-$\frac{1}{2}$m2•(m-$\frac{m}{2}$)=$\frac{2}{3}$,
即有$\frac{1}{3}$x3|${\;}_{0}^{m}$-$\frac{1}{4}$m3=$\frac{2}{3}$,
即为$\frac{1}{3}$m3-$\frac{1}{4}$m3=$\frac{2}{3}$,解得m=2,
即有A(2,4).
故选:B.
点评 本题考查导数的运用:求切线的方程,考查面积的求法,运用定积分和三角形的面积公式是解题的关键,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
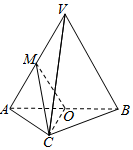 如图,在三棱锥V-ABC中,平面VA B⊥平面 ABC,AC=BC,O,M分别为A B,VA的中点.
如图,在三棱锥V-ABC中,平面VA B⊥平面 ABC,AC=BC,O,M分别为A B,VA的中点.