题目内容
11.给出下列命题:①对空间任意两个向量$\overrightarrow a,\overrightarrow b$($\overrightarrow b$≠$\overrightarrow 0$),则$\overrightarrow a$∥$\overrightarrow b$的充要条件是存在实数λ,使得$\overrightarrow b=λ\overrightarrow a$;
②若$\overrightarrow a•\overrightarrow b=0$,则$\overrightarrow a=\overrightarrow 0或\overrightarrow b=\overrightarrow 0$;
③若$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$不能构成空间的一个基底,则O,A,B,C四点共面;
④对于非零向量$\overrightarrow a,\overrightarrow b,\overrightarrow c$,则$(\overrightarrow a•\overrightarrow b)\overrightarrow c=\overrightarrow a(\overrightarrow b•\overrightarrow c)$一定成立.
正确命题的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据共线向量基本定理及向量垂直的充要条件即可判断出①②都为假命题,而根据基底的定义即可判断出③命题正确,而根据向量数乘的几何意义即可判断命题④为假命题,这样即可得出正确选项.
解答 解:①根据共线向量基本定理,$\overrightarrow{a}∥\overrightarrow{b}$的充要条件是存在实数λ,使得$\overrightarrow{b}=λ\overrightarrow{a}$,其中$\overrightarrow{a}≠\overrightarrow{0}$;
∵本命题没限制$\overrightarrow{a}≠\overrightarrow{0}$;
∴本命题为假命题;
②若$\overrightarrow{a}•\overrightarrow{b}=0$,则$\overrightarrow{a}⊥\overrightarrow{b}$,其中$\overrightarrow{a},\overrightarrow{b}$可以都为非零向量;
∴该命题为假命题;
③若$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$不能构成空间的一个基底,则$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$共面;
∴O,A,B,C四点共面;
∴该命题正确;
④$\overrightarrow{a},\overrightarrow{c}$不共线,且$\overrightarrow{a}•\overrightarrow{b}≠0$时,$(\overrightarrow{a}•\overrightarrow{b})\overrightarrow{c}≠\overrightarrow{a}(\overrightarrow{b}•\overrightarrow{c})$;
∴该命题为假命题;
∴正确命题个数为1.
故选A.
点评 考查共线向量基本定理,向量垂直的充要条件,以及空间基底的定义,共面向量的定义,向量数乘的几何意义.

| A. | [-3,5] | B. | [3,5] | C. | [-5,3] | D. | [-5,-3] |
| A. | 平行的两条直线的斜率一定相等 | B. | 平行的两条直线的倾斜角一定相等 | ||
| C. | 垂直的两直线的斜率之积为-1 | D. | 斜率相等的两条直线一定平行 |
| A. | (5,-3) | B. | (3,-5) | C. | (-5,3) | D. | (-5,-3) |
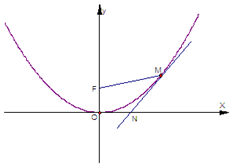 如图,抛物线x2=4y在点$M(t,\;\frac{1}{4}{t^2})\;(t>0)$处的切线与x轴相交于点N,O、F分别为该抛物线的顶点、焦点.
如图,抛物线x2=4y在点$M(t,\;\frac{1}{4}{t^2})\;(t>0)$处的切线与x轴相交于点N,O、F分别为该抛物线的顶点、焦点.