题目内容
若直线l过抛物线y2=4x的焦点F,交抛物线于A、B两点,且点B在x轴下方,若直线l的倾斜角θ≤
,则|FB|的取值范围是 .
| 3π |
| 4 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设B(x1,y1),依题意可求得抛物线y2=4x的焦点F(1,0)与准线方程x=-1;利用抛物线的定义,将|BF|转化为点A到其准线的距离,通过解方程组即可求得|FB|的最大值,从而可得|BF|的取值范围.
解答:
解:设B(x1,y1),依题意可求得抛物线y2=4x的焦点F(1,0)与准线方程x=-1;
利用抛物线的定义,|FB|=x1+1.
当AB的倾斜角θ=0°时,x1=0,|FB|=1,此时直线和抛物线只有一个交点,与题意不符;
当AB的倾斜角θ=135°时,|FB|最大,此时直线FB的方程为:y=-(x-1)=1-x.
由
可得x=3+2
,或 x=3-2
(舍去),
故∴|BF|的取值范围是(1,3+2
],
故答案为:(1,3+2
].
利用抛物线的定义,|FB|=x1+1.
当AB的倾斜角θ=0°时,x1=0,|FB|=1,此时直线和抛物线只有一个交点,与题意不符;
当AB的倾斜角θ=135°时,|FB|最大,此时直线FB的方程为:y=-(x-1)=1-x.
由
|
| 2 |
| 2 |
故∴|BF|的取值范围是(1,3+2
| 2 |
故答案为:(1,3+2
| 2 |
点评:本题考查抛物线的简单性质,考查方程思想与等价转化思想,考查运算能力,属于基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如图,设O为?ABCD所在平面外任意一点,E为OC的中点,若
如图,设O为?ABCD所在平面外任意一点,E为OC的中点,若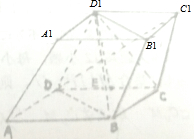 如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为a的正方形,D1是底面ABCD上的射影E恰好是CD的中点,BD1⊥DC1.
如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为a的正方形,D1是底面ABCD上的射影E恰好是CD的中点,BD1⊥DC1.