题目内容
9.在△ABC中,M为AB的中点,$\overrightarrow{AN}=2\overrightarrow{NC}$,若$\overrightarrow{MN}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则x+y=$\frac{1}{6}$
分析 用$\overrightarrow{AB}、\overrightarrow{AC}$表示$\overrightarrow{MN}$即可求出x、y.
解答 解:∵M为AB的中点,$\overrightarrow{AN}=2\overrightarrow{NC}$,∴$\overrightarrow{MN}=\overrightarrow{AN}-\overrightarrow{AM}=\frac{2}{3}\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AB}$,⇒x=-$\frac{1}{2}$,y=$\frac{2}{3}$,∴x+y=$\frac{1}{6}$;
故答案为:$\frac{1}{6}$
点评 本题考查了平面向量的线性运算,属于基础题.

练习册系列答案
相关题目
20.已知直线ax-ky+k=0(a为常数,k≠0为参数),不论k取何值,直线总过定点( )
| A. | (a,0) | B. | (1,0) | C. | (1,1) | D. | (0,1) |
17.设点A(3,-5),B(-2,-2),直线l过点P(1,1)且与线段AB相交,则直线l的斜率k的取值范围是( )
| A. | k≥1或k≤-3 | B. | -3≤k≤1 | C. | -1≤k≤3 | D. | 以上都不对 |
14.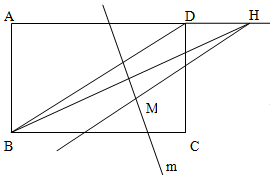 如图所示,ABCD是长为8,宽为4的矩形,设点H在直线AD上运动,BH的垂直平分线为m,过点H且与BD平行(或重合)的直线与直线m相交于点M,则点M的轨迹为( )
如图所示,ABCD是长为8,宽为4的矩形,设点H在直线AD上运动,BH的垂直平分线为m,过点H且与BD平行(或重合)的直线与直线m相交于点M,则点M的轨迹为( )
 如图所示,ABCD是长为8,宽为4的矩形,设点H在直线AD上运动,BH的垂直平分线为m,过点H且与BD平行(或重合)的直线与直线m相交于点M,则点M的轨迹为( )
如图所示,ABCD是长为8,宽为4的矩形,设点H在直线AD上运动,BH的垂直平分线为m,过点H且与BD平行(或重合)的直线与直线m相交于点M,则点M的轨迹为( )| A. | 圆的一部分 | B. | 椭圆的一部分 | C. | 双曲线的一部分 | D. | 抛物线的一部分 |