题目内容
4.若函数f(x)=ax3-bx+2,a,b∈R若f(-2)=-1,则f(2)=5.分析 根据函数奇偶性的性质建立方程关系进行求解即可.
解答 解:∵f(-2)=-1,
∴f(-2)=-8a+2b+2=-1,
即8a-2b=3,
则f(2)=8a-2b+2=3+2=5,
故答案为:5
点评 本题主要考查函数值的计算,根据函数奇偶性的性质建立方程关系是解决本题的关键.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
14.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线为$y=-\sqrt{2}x$,且一个焦点是抛物线y2=12x的焦点,则该双曲线的方程为( )
| A. | $\frac{y^2}{3}-\frac{x^2}{6}=1$ | B. | $\frac{x^2}{3}-\frac{y^2}{6}=1$ | C. | $\frac{x^2}{6}-\frac{y^2}{3}=1$ | D. | $\frac{y^2}{6}-\frac{x^2}{3}=1$ |
15.下列在曲线$\left\{\begin{array}{l}x=cosθ+sinθ\\ y=sin2θ\end{array}$(θ为参数)上的点是( )
| A. | $(\frac{1}{2},-\sqrt{2})$ | B. | $(2,\sqrt{3})$ | C. | $(\sqrt{2},1)$ | D. | $(1,\sqrt{3})$ |
12.设a>0且a≠1,则“函数f(x)=ax”在R上是增函数是“函数g(x)=xa”“在(0,+∞)上是增函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.已知定点M(-3,0),N(2,0),如果动点P满足|PM|=2|PN|,则点P的轨迹所包围的图形面积等于( )
| A. | $\frac{100π}{9}$ | B. | $\frac{142π}{9}$ | C. | $\frac{10π}{3}$ | D. | 9π |
16.在某化学反应的中间阶段,压力保持不变,温度从1°变化到5°,反应结果如下表所示(x代表温度,y代表结果):
(1)求化学反应的结果y对温度x的线性回归方程$\widehaty=\widehatbx+\widehata$;
(2)判断变量x与y之间是正相关还是负相关,并预测当温度达到10°时反应结果为多少?
| x | 1 | 2 | 3 | 4 | 5 |
| y | 3 | 5 | 7 | 10 | 11 |
(2)判断变量x与y之间是正相关还是负相关,并预测当温度达到10°时反应结果为多少?
13.某几何体三视图如图所示,则该几何体的表面积为( )
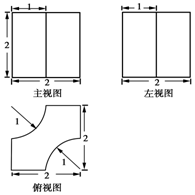

| A. | 8+2π | B. | 16+2π | C. | 20+2π | D. | 16+π |
14.在等差数列{an}中,a3+a6=11,a5+a8=39,则公差d为( )
| A. | -14 | B. | -7 | C. | 7 | D. | 14 |
