题目内容
1.等比数列{an}中的a1,a2015是函数f(x)=$\frac{1}{3}$x3-4x2+4x-1的极值点,则log2a1+log2a2+…+log2a2015=( )| A. | 4032 | B. | 4030 | C. | 2016 | D. | 2015 |
分析 利用对数函数的运算性质与等比数列的性质即可求的log2a1+log2a2+…+log2a2015的值.
解答 解:f′(x)=x2-8x+4,
∵a1、a2015是函数f(x)的极值点,
∴a1、a2015是方程x2-8x+4=0的两实数根,则a1•a2015=4,
∴a1008=2,
∴log2a1+log2a2+…+log2a2015=${log}_{2}^{{(a}_{1}{•a}_{2}…{•a}_{2015})}$=${log}_{2}^{{{(a}_{1008})}^{2015}}$=2015,
故选:D.
点评 本题考查对数函数的运算性质与等比数列的性质,得到a1•a2•…•a2015是=${{(a}_{1008})}^{2015}$关键,属于中档题.

练习册系列答案
相关题目
10.已知a>0,b>0,若a+b=4,则( )
| A. | a2+b2有最小值 | B. | $\sqrt{ab}$有最小值 | C. | $\frac{1}{a}+\frac{1}{b}$有最大值 | D. | $\frac{1}{{\sqrt{a}+\sqrt{b}}}$有最大值 |
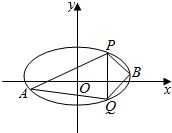 已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{1}{2}$,且椭圆的短轴长为4$\sqrt{3}$.
已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{1}{2}$,且椭圆的短轴长为4$\sqrt{3}$.