题目内容
10．已知a＞0，b＞0，若a+b=4，则（ ）| A． | a2+b2有最小值 | B． | $\sqrt{ab}$有最小值 | C． | $\frac{1}{a}+\frac{1}{b}$有最大值 | D． | $\frac{1}{{\sqrt{a}+\sqrt{b}}}$有最大值 |
分析 根据基本不等式的性质判断即可．
解答 解：∵a＞0，b＞0，且a+b=4，
a2+b2=（a+b）2-2ab=16-2ab≥16-2$\sqrt{\frac{a+b}{2}}$=16-2$\sqrt{2}$，
有最小值，
故选：A．
点评 本题考察了基本不等式的性质，是一道基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1．等比数列{an}中的a1，a2015是函数f（x）=$\frac{1}{3}$x3-4x2+4x-1的极值点，则log2a1+log2a2+…+log2a2015=（ ）
| A． | 4032 | B． | 4030 | C． | 2016 | D． | 2015 |
5．下列函数中，是奇函数且在（0，+∞）上单调递增的为（ ）
| A． | y=x2 | B． | $y={x^{\frac{1}{3}}}$ | C． | y=x-1 | D． | $y={x^{-\frac{1}{2}}}$ |
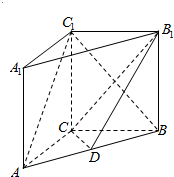如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，AC=3，BC=4，AA1=4，点D是AB的中点，