题目内容
13.已知向量$\overrightarrow{m}$=(3sinx,cosx),$\overrightarrow{n}$=(-cosx,$\sqrt{3}$cosx),f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$-$\frac{\sqrt{3}}{2}$.(I)求函数f(x)的最大值及取得最大值时x的值;
(Ⅱ)若方程f(x)=a在区间[0,$\frac{π}{2}$]上有两个不同的实数根,求实数a的取值范围.
分析 (Ⅰ)根据向量的数量积运算,化简得到f(x)=$\sqrt{3}$sin(2x+$\frac{5π}{6}$),根据三角函数的性质求出最值,
(Ⅱ)求出函数f(x)的单调区间,并画出y=f(x)和y=a的图象,由图象可得到答案.
解答 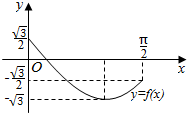 解:(Ⅰ)f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$-$\frac{\sqrt{3}}{2}$=-3sinxcosx+$\sqrt{3}$cos2x-$\frac{\sqrt{3}}{2}$=-$\frac{3}{2}$sin2x+$\frac{\sqrt{3}}{2}$(1+cos2x)-$\frac{\sqrt{3}}{2}$=-$\frac{3}{2}$sin2x+$\frac{\sqrt{3}}{2}$cos2x=$\sqrt{3}$sin(2x+$\frac{5π}{6}$)
解:(Ⅰ)f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$-$\frac{\sqrt{3}}{2}$=-3sinxcosx+$\sqrt{3}$cos2x-$\frac{\sqrt{3}}{2}$=-$\frac{3}{2}$sin2x+$\frac{\sqrt{3}}{2}$(1+cos2x)-$\frac{\sqrt{3}}{2}$=-$\frac{3}{2}$sin2x+$\frac{\sqrt{3}}{2}$cos2x=$\sqrt{3}$sin(2x+$\frac{5π}{6}$)
当2x+$\frac{5π}{6}$=2kπ+$\frac{π}{2}$,即x=kπ-$\frac{π}{6}$,k∈Z时,函数f(x)取得最大值$\sqrt{3}$,
(Ⅱ)由于x∈[0,$\frac{π}{2}$]时,2x+$\frac{5π}{6}$∈[$\frac{5π}{6}$,$\frac{11π}{6}$],
而函数f(x)在区间[$\frac{5π}{6}$,$\frac{3π}{2}$]上单调递减,在区间[$\frac{3π}{2}$,$\frac{11π}{6}$]上单调递增,
结合图象(如图),所以方程f(x)=a在区间[0,$\frac{π}{2}$]上有两个不同的实数根时,a∈(-$\sqrt{3}$,-$\frac{\sqrt{3}}{2}$].
点评 本题考查了向量的运算和三角函数的化简,以及参数的取值范围,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 4032 | B. | 4030 | C. | 2016 | D. | 2015 |
| A. | y=x2 | B. | $y={x^{\frac{1}{3}}}$ | C. | y=x-1 | D. | $y={x^{-\frac{1}{2}}}$ |
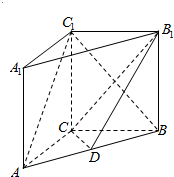 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=3,BC=4,AA1=4,点D是AB的中点,
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=3,BC=4,AA1=4,点D是AB的中点,