题目内容
4.直线x-2017=0的倾斜角为( )| A. | 0 | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | 不存在 |
分析 直线x-2017=0与x轴垂直,由此能求出直线x-2017=0的倾斜角.
解答 解:∵直线x-2017=0与x轴垂直,
∴直线x-2017=0的倾斜角为$\frac{π}{2}$.
故选:C.
点评 本题考查直线的倾斜角的求法,是基础题,解题时要注意直线方程的性质的合理运用.

练习册系列答案
相关题目
19.已知F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐角三角形,则双曲线的离心率的取值范围是( )
| A. | (1,+∞) | B. | $(1,1+\sqrt{2})$ | C. | $(1,\sqrt{3})$ | D. | $(1-\sqrt{2},1+\sqrt{2})$ |
16.若变量x,y满足条件$\left\{\begin{array}{l}3x-y≤0\\ x-3y+5≥0\\ x≥0\end{array}\right.$则z=x+y的最大值为( )
| A. | $\frac{5}{2}$ | B. | 2 | C. | $\frac{5}{3}$ | D. | 0 |
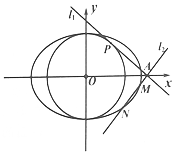 已知椭圆C:$\frac{{x}^{2}}{2}+{y}^{2}=1$和圆O:x2+y2=1,过点A(m,0)(m>1)作两条互相垂直的直线l1,l2,l1于圆O相切于点P,l2与椭圆相交于不同的两点M,N.
已知椭圆C:$\frac{{x}^{2}}{2}+{y}^{2}=1$和圆O:x2+y2=1,过点A(m,0)(m>1)作两条互相垂直的直线l1,l2,l1于圆O相切于点P,l2与椭圆相交于不同的两点M,N.