题目内容
已知两圆x2＋y2－2x－6y－1＝0和x2＋y2－10x－12y＋m＝0.
(1)m取何值时两圆外切？
(2)m取何值时两圆内切？
(3)求m＝45时两圆的公共弦所在直线的方程和公共弦的长．
解 两圆的标准方程为：(x－1)2＋(y－3)2＝11，(x－5)2＋(y－6)2＝61－m，
圆心分别为M(1,3)，N(5,6)，半径分别为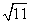
和
.
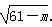(1)当两圆外切时，
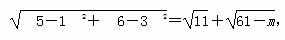解得m＝25＋10.
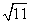(2)当两圆内切时，因定圆的半径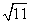小于两圆圆心间距离5，故只有
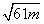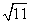－＝5，解得m＝25－10.
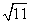(3)两圆的公共弦所在直线方程为
(x2＋y2－2x－6y－1)－(x2＋y2－10x－12y＋45)＝0，
即4x＋3y－23＝0，
∴公共弦长为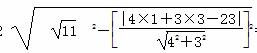2 
＝2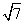
.
练习册系列答案
名校课堂系列答案
相关题目
的圆的方程．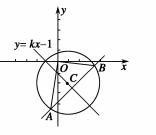
＋
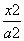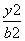＝1(a>b>0)的左焦点为F，离心率为
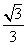，过点F且与x轴垂直的直线被椭圆截得的线段长为
.
＋
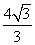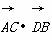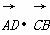＝8，求k的值．
－
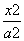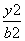＝1(a，b＞0)的两顶点为A1，A2，虚轴两端点为B1，B2，
＝________.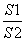