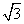题目内容
根据下列条件,求圆的方程.
求过P(4,-2),Q(-1,3)两点,且在y轴上截得的线段长为4 的圆的方程.
的圆的方程.
设圆的方程为x2+y2+Dx+Ey+F=0(D2+E2-4F>0).①
将P,Q点的坐标分别代入①得
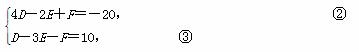
令x=0,由①得y2+Ey+F=0.④
由已知|y1-y2|=4 ,其中y1,y2是方程④的两根,
,其中y1,y2是方程④的两根,
所以(y1-y2)2=(y1+y2)2-4y1y2=E2-4F=48.⑤
解②、③、⑤组成的方程组得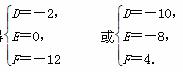
故所求圆的方程为x2+y2-2x-12=0或x2+y2-10x-8y+4=0

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目

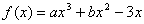 在
在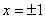 处取得极值.
处取得极值.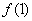 和
和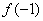 是函数
是函数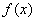 的极大值还是极小值;
的极大值还是极小值;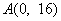 作曲线
作曲线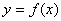 的切线,求此切线方程.
的切线,求此切线方程.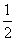 时,直线l1:kx-y=k-1与直线l2:ky-x=2k的交点在( ).
时,直线l1:kx-y=k-1与直线l2:ky-x=2k的交点在( ).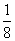 ,则这两条直线之间的距离的最大值和最小值分别为( ).
,则这两条直线之间的距离的最大值和最小值分别为( ).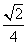 ,
,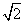 ,
,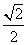 C.
C.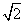 B.2
B.2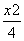 +
+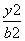 =1(0<b<2),左、右焦点分别为F1,F2,过F1的直线l交椭圆于A,B两点,若|BF2|+|AF2|的最大值为5,则b的值是( ).
=1(0<b<2),左、右焦点分别为F1,F2,过F1的直线l交椭圆于A,B两点,若|BF2|+|AF2|的最大值为5,则b的值是( ).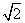 C.
C.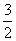 D.
D.