题目内容
设f(x)=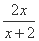 ,x1=1,xn=f(
,x1=1,xn=f(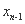 )(n≥2,n∈N+).
)(n≥2,n∈N+).
(1) 求x2,x3,x4的值;
(2) 归纳并猜想{xn}的通项公式;
(3) 用数学归纳法证明你的猜想.
(1) x2=f(x1)= ,x3=f(x2)=
,x3=f(x2)= =
= =
= ,x4=f(x3)=
,x4=f(x3)= =
= .
.
(2) 根据计算结果,可以归纳猜想出xn= .
.
(3) ①当n=1时,x1= =1,与已知相符,归纳出的公式成立.
=1,与已知相符,归纳出的公式成立.
②假设当n=k(k∈N+)时,公式成立,
即xk= ;那么,当n=k+1时,有
;那么,当n=k+1时,有
 =f(xk)=
=f(xk)= =
= =
= =
= ,
,
所以,当n=k+1时公式也成立.
由①②知,对任意n∈N+,有xn= 成立.
成立.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
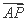 =
=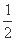 sin2θ·
sin2θ·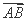 +cos2θ·
+cos2θ·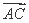 (θ∈R),则(
(θ∈R),则(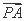 +
+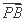 )·
)·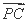 的最小值是 .
的最小值是 . 
 为等差数列,若
为等差数列,若 <-1,且它们的前n项和Sn有最大值,则使得Sn>0的n的最大值为 .
<-1,且它们的前n项和Sn有最大值,则使得Sn>0的n的最大值为 .  +
+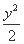 =1的焦点为F1,F2,点P在椭圆上,若PF1=4,则∠F1PF2的大小为 .
=1的焦点为F1,F2,点P在椭圆上,若PF1=4,则∠F1PF2的大小为 .