题目内容
将函数f（x）=2
sin（π-x）sin（
+x）-sin（
-2x）的图象向右平移φ（φ＞0）个单位，所得函数图象的一条对称轴为x=
，则φ的最小值为（ ）
| 3 |
| π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：三角函数中的恒等变换应用,正弦函数的图象
专题：三角函数的图像与性质
分析：利用两角和差的正弦公式，结合诱导公式以及辅助角公式将函数进行化简即可得到结论．
解答：
解：f（x）=2
sin（π-x）sin（
+x）-sin（
-2x）=2
sinxcosx+cos2x=
sin2x+cos2x=2sin（2x+
），
将f（x）的图象向右平移φ（φ＞0）个单位得到y=2sin[2（x-φ）+
]=2sin（2x-2φ+
），
若所得函数图象的一条对称轴为x=
，
则当x=
时，2×
-2φ+
=
+kπ，
即φ=
-
，k∈Z，
∵φ＞0，
∴当k=0时，φ=
，
故选：B
| 3 |
| π |
| 2 |
| 3π |
| 2 |
| 3 |
| 3 |
| π |
| 6 |
将f（x）的图象向右平移φ（φ＞0）个单位得到y=2sin[2（x-φ）+
| π |
| 6 |
| π |
| 6 |
若所得函数图象的一条对称轴为x=
| π |
| 2 |
则当x=
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
即φ=
| π |
| 3 |
| kπ |
| 2 |
∵φ＞0，
∴当k=0时，φ=
| π |
| 3 |
故选：B
点评：本题主要考查三角函数的图象和性质，利用辅助角公式以及函数图象平移关系是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
若过点A（3，0）的直线l与圆（x-1）2+y2=1有公共点，则直线l的斜率的取值范围为（ ）
A、[-
| ||||||||
B、（-
| ||||||||
C、[-
| ||||||||
D、（-
|
函数y=
在区间（k-1，k+1）上是单调函数，则实数k的取值范围是（ ）
| x |
| x+1 |
| A、（-2，0） |
| B、[-2，0] |
| C、（-∞，-2）∪（0，+∞） |
| D、（-∞，-2]∪[0，+∞） |
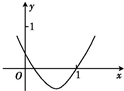如图是二次函数f（x）=| 1 |
| 2 |
A、（
| ||||
B、（
| ||||
| C、（1，2） | ||||
| D、（2，3） |