题目内容
已知f(x)=ex-t(x+1).
(1)若f(x)≥0对一切正实数x恒成立,求t的取值范围;
(2)设g(x)=f(x)+
,且A(x1,y1)、B(x2,y2)(x1≠x2)是曲线y=g(x)上任意两点,若对任意的t≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
(3)求证:1n+2n+…+(n-1)n≤nn(n∈N*).
(1)若f(x)≥0对一切正实数x恒成立,求t的取值范围;
(2)设g(x)=f(x)+
| t |
| ex |
(3)求证:1n+2n+…+(n-1)n≤nn(n∈N*).
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)f(x)≥0?t≤
(x>0)恒成立.设p(x)=
(x≥0),则p′(x)=
≥0,从而求出p(x)在x∈[0,+∞]单调递增,p(x)≥p(0)=1(x=1时取等号),进而t≤1;
(2)设x1、x2是任意的两实数,且x1<x2
>m,故g(x2)-mx2>g(x1)-mx1设F(x)=g(x)-mx,则F(x)在R上单增,而g′(x)=ex-t-
≥2
-t=-t+2
=(
+1)2≥3故m<3;
(3)由(1)知,x+1≤ex=e(x+1)-1,∴x≤ex-1取x=
(k=1,2,…,n-1),则(
)n≤(e
-1)n=
.从而1n+2n+…+(n-1)n≤nn(n∈N*).
| ex |
| x+1 |
| ex |
| x+1 |
| xex |
| (x+1)2 |
(2)设x1、x2是任意的两实数,且x1<x2
| g(x2)-g(x1) |
| x2-x1 |
| t |
| ex |
ex•(
|
| -t |
| -t |
(3)由(1)知,x+1≤ex=e(x+1)-1,∴x≤ex-1取x=
| k |
| n |
| k |
| n |
| k |
| n |
| ek |
| en |
解答:
解:(1)f(x)≥0?t≤
(x>0)恒成立.
设p(x)=
(x≥0),则p′(x)=
≥0
∴p(x)在x∈[0,+∞]单调递增,p(x)≥p(0)=1(x=1时取等号),
∴t≤1;
(2)设x1、x2是任意的两实数,且x1<x2
>m,
故g(x2)-mx2>g(x1)-mx1
设F(x)=g(x)-mx,
则F(x)在R上单增,
即F'(x)=g'(x)-m>0恒成立.
即对任意的t≤-1,x∈R,m<g'(x)恒成立.
而g′(x)=ex-t-
≥2
-t=-t+2
=(
+1)2-1≥3,
故m<3;
(3)由(1)知,x+1≤ex,∴x≤ex-1,
取x=
(k=1,2,…,n-1),
则(
)n≤(e
-1)n=
.
(
)n≤
=
•
=
(
-
)<
<1,
(
)n<1, ∴
kn<nn,
∴1n+2n+…+(n-1)n≤nn(n∈N*)
| ex |
| x+1 |
设p(x)=
| ex |
| x+1 |
| xex |
| (x+1)2 |
∴p(x)在x∈[0,+∞]单调递增,p(x)≥p(0)=1(x=1时取等号),
∴t≤1;
(2)设x1、x2是任意的两实数,且x1<x2
| g(x2)-g(x1) |
| x2-x1 |
故g(x2)-mx2>g(x1)-mx1
设F(x)=g(x)-mx,
则F(x)在R上单增,
即F'(x)=g'(x)-m>0恒成立.
即对任意的t≤-1,x∈R,m<g'(x)恒成立.
而g′(x)=ex-t-
| t |
| ex |
ex•(
|
| -t |
| -t |
故m<3;
(3)由(1)知,x+1≤ex,∴x≤ex-1,
取x=
| k |
| n |
则(
| k |
| n |
| k |
| n |
| ek |
| en |
| n-1 |
 |
| k=1 |
| k |
| n |
| n-1 |
 |
| k=1 |
| ek |
| en |
| 1 |
| en |
| e(1-en-1) |
| 1-e |
| e |
| e-1 |
| 1 |
| e |
| 1 |
| en |
| 1 |
| e-1 |
| n-1 |
 |
| k=1 |
| k |
| n |
| n-1 |
 |
| k=1 |
∴1n+2n+…+(n-1)n≤nn(n∈N*)
点评:本题考察了函数的单调性,函数的最值问题,求参数的范围,不等式的证明,导数的应用,有一定的难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
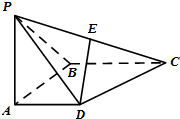 如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,且∠PAB=∠ABC=90°,AD∥BC,PA=AB=BC=2AD,E是PC的中点.
如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,且∠PAB=∠ABC=90°,AD∥BC,PA=AB=BC=2AD,E是PC的中点.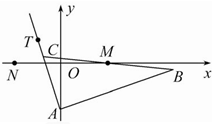 已知△ABC的边AB所在直线的方程为x-3y-6=0,M(2,0)满足
已知△ABC的边AB所在直线的方程为x-3y-6=0,M(2,0)满足