题目内容
椭圆方程为
+
=1（a＞b＞0）的一个顶点为A（0，2），离心率e=
．
（1）求椭圆的方程；
（2）直线l：y=kx-2（k≠0）与椭圆相交于不同的两点M，N满足
=
，
•
=0，求k．
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
（1）求椭圆的方程；
（2）直线l：y=kx-2（k≠0）与椭圆相交于不同的两点M，N满足
| MP |
| PN |
| AP |
| MN |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：（1）由于椭圆
+
=1（a＞b＞0）的一个顶点为A（0，2），离心率e=
．可得b=2，
=
，又a2=b2+c2，解得a2，即可得出椭圆的方程．
（2）如图所示，把直线方程与椭圆方程联立可得（1+3k2）x2-12kx=0．解出可得M，N的坐标．由于M，N满足
=
，
•
=0，可得点P是线段MN的中点，AP⊥MN．
利用中点坐标公式、相互垂直的直线与斜率之间的关系即可得出．
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| c |
| a |
| ||
| 3 |
（2）如图所示，把直线方程与椭圆方程联立可得（1+3k2）x2-12kx=0．解出可得M，N的坐标．由于M，N满足
| MP |
| PN |
| AP |
| MN |
利用中点坐标公式、相互垂直的直线与斜率之间的关系即可得出．
解答：
解：（1）∵椭圆
+
=1（a＞b＞0）的一个顶点为A（0，2），离心率e=
．
∴b=2，
=
，又a2=b2+c2，解得a2=12，c2=8．
∴椭圆的方程为：
+
=1．
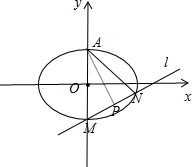
（2）如图所示，
联立
，化为（1+3k2）x2-12kx=0．
解得
，或
，
取M（0，-2），N(
，
)．
∵M，N满足
=
，
•
=0，
∴点P是线段MN的中点，AP⊥MN．
∴P(
，
)，
∴kAP=
．
∴
•k=-1，
解得k=±
．
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
∴b=2，
| c |
| a |
| ||
| 3 |
∴椭圆的方程为：
| x2 |
| 12 |
| y2 |
| 4 |
（2）如图所示，
联立
|
解得
|
|
取M（0，-2），N(
| 12k |
| 1+3k2 |
| 6k2-2 |
| 1+3k2 |
∵M，N满足
| MP |
| PN |
| AP |
| MN |
∴点P是线段MN的中点，AP⊥MN．
∴P(
| 6k |
| 1+3k2 |
| -2 |
| 1+3k2 |
∴kAP=
| -2-3k2 |
| 3k |
∴
| -2-3k2 |
| 3k |
解得k=±
| ||
| 3 |
点评：本题考查了椭圆的标准方程及其性质、中点坐标公式、相互垂直的直线与斜率之间的关系、数量积运算性质，考查了推理能力与计算能力，属于难题．
练习册系列答案
阅读快车系列答案
相关题目
如图，四棱锥P-ABCD中，ABCD为矩形，△PAD为等腰直角三角形，∠APD=90°，平面PAD⊥平面ABCD，AB=1，AD=2，E，F分别是PC和BD的中点．已知函数f（x）=ln
满足f（1）=0，且对任何正数x，都有f（x）-f（
）=lnx．
（1）求实数a，b的值；
（2）若关于x的方程f（x）=ln（m+x）无实数解，求实数m的取值范围．
| 2x |
| ax+b |
| 1 |
| x |
（1）求实数a，b的值；
（2）若关于x的方程f（x）=ln（m+x）无实数解，求实数m的取值范围．
已知某几何体的三视图如图所示，则该几何体的体积为（ ）
| A、6π | ||
B、
| ||
| C、3π | ||
D、
|
高为2的直三棱柱的俯视图是一个边长为2的正三角形，如图所示，则这个直三棱柱的正视图的面积是（ ）
| A、4 | ||
B、2
| ||
| C、3 | ||
| D、2 |