题目内容
已知数列{an}前项n和sn=n2+4n(n∈N*),数列{bn}为等比数列,首项b1=2,公比为q(q>0),且满足b2,b3+4q,b4成等差数列.
(1)求数列{an},{bn}的通项公式;
(2)设cn=
,记数列{cn}的前n项和为Tn,求Tn.
(1)求数列{an},{bn}的通项公式;
(2)设cn=
| 3(an-3)•bn |
| 4 |
考点:数列的求和,等差数列与等比数列的综合
专题:等差数列与等比数列
分析:(1)利用已知条件和等量关系求出数列的通项公式.
(2)利用(1)的结论,进一步求出数列的通项公式,利用乘公比错位相减法求数列的和.
(2)利用(1)的结论,进一步求出数列的通项公式,利用乘公比错位相减法求数列的和.
解答:
解(Ⅰ)当n=1时,a1=S1=5.
当n≥2时,an=Sn-Sn-1=2n+3
验证n=1时也成立.∴数的通项公式为:an=2n+3,
∵b2,b3+4q,b4成等差数列,b1=2.
所以2(b3+4q)=b2+b4,
即q2-2q-3=0,
因为q>0,
∴q=3.
∴
∴数的通项公式为:b=2•3n-1.
(Ⅱ)∵cn=
=n•3n
∴Tn=c1+c2+…+cn=1•31+2•32+…+n•3n①
3Tn=1•32+2•33+…+n•3n+1②
①-②得:
Tn=
当n≥2时,an=Sn-Sn-1=2n+3
验证n=1时也成立.∴数的通项公式为:an=2n+3,
∵b2,b3+4q,b4成等差数列,b1=2.
所以2(b3+4q)=b2+b4,
即q2-2q-3=0,
因为q>0,
∴q=3.
∴
|
∴数的通项公式为:b=2•3n-1.
(Ⅱ)∵cn=
| 3(an-3)bn |
| 4 |
∴Tn=c1+c2+…+cn=1•31+2•32+…+n•3n①
3Tn=1•32+2•33+…+n•3n+1②
①-②得:
Tn=
| (2n-1)3n+1+3 |
| 4 |
点评:本题考查的知识要点:数列的通项公式的求法,利用乘公比错位相减法求数列的和.属于基础题型.

练习册系列答案
相关题目
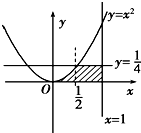
由曲线y=x2和直线y=0,x=1,y=
所围成的封闭图形的面积为( )
| 1 |
| 4 |

A、
| ||
B、
| ||
C、
| ||
D、
|