题目内容
15.已知函数$f(x)={sin^2}x+\sqrt{3}sinxcosx-\frac{1}{2}$.(1)求f(x)单调递减区间;
(2)已知a,b,c分别为△ABC内角,A,B,C的对边,$a=2\sqrt{3},c=4,若f(A)$是f(x)在(0,π)上的最大值,求△ABC的面积.
分析 (1)由三角函数公式化简可得f(x)=sin(2x-$\frac{π}{6}$),解不等式2kπ+$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$可可得单调减区间;
(2)由题意可得A=$\frac{π}{3}$,由余弦定理可得b=2,代值计算可.
解答 解:(1)化简可得f(x)=sin2x+$\sqrt{3}$sinxcosx-$\frac{1}{2}$.
=$\frac{1}{2}$(1-cos2x)+$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$cos2x
=sin(2x-$\frac{π}{6}$),
由2kπ+$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$可得kπ+$\frac{π}{3}$≤x≤kπ+$\frac{5π}{6}$,
∴f(x)的单调减区间为[kπ+$\frac{π}{3}$,kπ+$\frac{5π}{6}$](k∈Z);
(2)由(1)知f(x)=sin(2x-$\frac{π}{6}$),
当x∈(0,π)时,-$\frac{π}{6}$<2x-$\frac{π}{6}$<$\frac{11π}{6}$,
结合正弦函数的图象,当2x-$\frac{π}{6}$=$\frac{π}{2}$,即x=$\frac{π}{3}$时,f(x)取得最大值,
∵f(A)是f(x)在(0,π)上的最大值,
∴A=$\frac{π}{3}$,
在△ABC中,由余弦定理可得a2=b2+c2-2bccosA,
即12=b2+16-2×4b×$\frac{1}{2}$,
解得b=2,
∴△ABC的面积S=$\frac{1}{2}$bcsinA=$\frac{1}{2}$×2×4sin$\frac{π}{3}$=2$\sqrt{3}$.
点评 本题考查解三角形,涉及两角和与差的三角函数公式余弦定理以及三角形的面积,属中档题.

 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | 2 |
| A. | f(-$\frac{3}{4}$)<f(a2-a+1) | B. | f(-$\frac{3}{4}$)>f(a2-a+1) | C. | f(-$\frac{3}{4}$)≤f(a2-a+1) | D. | f(-$\frac{3}{4}$)≥f(a2-a+1) |
| A. | (1)(3) | B. | (2)(4) | C. | (2)(3)(4) | D. | (1)(2)(3)(4) |
| A. | 直线x=1对称 | B. | 直线x=-1对称 | C. | 点(1,0)对称 | D. | 点(-1,0)对称 |
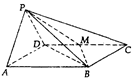 如图,在四棱锥中P-ABCD中,底面ABCD是菱形,且∠DAB=60°,PA=PD,M为CD的中点,平面PAD⊥平面ABCD.
如图,在四棱锥中P-ABCD中,底面ABCD是菱形,且∠DAB=60°,PA=PD,M为CD的中点,平面PAD⊥平面ABCD.