题目内容
7.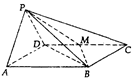 如图,在四棱锥中P-ABCD中,底面ABCD是菱形,且∠DAB=60°,PA=PD,M为CD的中点,平面PAD⊥平面ABCD.
如图,在四棱锥中P-ABCD中,底面ABCD是菱形,且∠DAB=60°,PA=PD,M为CD的中点,平面PAD⊥平面ABCD.(1)求证:BD⊥PM;
(2)若∠APD=90°,PA=$\sqrt{2}$,求点A到平面PBM的距离.
分析 (1)取AD中点E,连接PE,EM,AC,证明:BD⊥平面PEM,即可证明BD⊥PM;
(2)利用等体积方法,求点A到平面PBM的距离.
解答  (1)证明:取AD中点E,连接PE,EM,AC,
(1)证明:取AD中点E,连接PE,EM,AC,
∵底面ABCD是菱形,
∴BD⊥AC,
∵E,M分别是AD,DC的中点,
∴EM∥AC,
∴EM⊥BD.
∵PA=AD,
∴PE⊥AD,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴PE⊥平面ABCD,
∴PE⊥BD,
∵EM∩PE=E,
∴BD⊥平面PEM,
∵PM?平面PEM,
∴BD⊥PM.
(2)解:∵PA=PD=$\sqrt{2}$,∠APD=90°,∠DAB=60°,
∴AD=AB=BD=2,PE=1,EM=$\frac{1}{2}AC$=$\sqrt{3}$,
∴PM=PB=$\sqrt{1+3}$=2.
等边三角形DBC中,BM=$\sqrt{3}$,∴S△PBM=$\frac{\sqrt{39}}{4}$,S△ABM=$\frac{1}{2}×2×\sqrt{3}$=$\sqrt{3}$.
设三棱锥A-PBM的高为h,则由等体积可得$\frac{1}{3}•\frac{\sqrt{39}}{4}h=\frac{1}{3}•\sqrt{3}•1$,
∴h=$\frac{4\sqrt{13}}{13}$,
∴点A到平面PBM的距离为$\frac{4\sqrt{13}}{13}$.
点评 本题考查线面垂直的判定与性质,考查点到平面距离的计算,考查等体积方法的运用,属于中档题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
17.已知数列{an}、{bn}满足bn=log2an,n∈N+,其中{bn}是等差数列,且a9a2009=4,则b1+b2+b3+…+b2017=( )
| A. | 2016 | B. | 2017 | C. | log22017 | D. | $\frac{2017}{2}$ |
12.双曲线mx2+y2=1(m∈R)的离心率为$\sqrt{2}$,则m的值为( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 2 |
17.已知复数z=$\frac{1+i}{1-i}$,则$\overline{z}$=( )
| A. | -2i | B. | -i | C. | 2i | D. | i |