题目内容
已知抛物线 的焦点为
的焦点为 ,过
,过 任作直线
任作直线 (
( 与
与 轴不平行)交抛物线分别于
轴不平行)交抛物线分别于 两点,点
两点,点 关于
关于 轴对称点为
轴对称点为 ,
,
(1)求证:直线 与
与 轴交点
轴交点 必为定点;
必为定点;
 (2)过
(2)过 分别作抛物线的切线,两条切线交于
分别作抛物线的切线,两条切线交于 ,求
,求 的最小值,并求当
的最小值,并求当 取最小值时直线
取最小值时直线 的方程。
的方程。
设 ,∵抛物线
,∵抛物线 的焦点为
的焦点为
 ∴可设直线
∴可设直线 的方程为:
的方程为:
 ,消去
,消去 并整理得:
并整理得:
 ……4分
……4分
 ,
,
直线 的方程为
的方程为

∴直线 与
与 轴交于定点
轴交于定点 …………7分
…………7分
(2)设过点 的切线方程为
的切线方程为 ,则
,则 得
得

即


∴过点 的切线方程为:
的切线方程为:
即: ③,同理可得过点
③,同理可得过点 的切线方程为:
的切线方程为:
 ④……9分
④……9分
③—④得: (
( )
)
∴
③+④得:

 ……12分
……12分
∴ ,
,

∴ ,取等号时,
,取等号时, ,
,
直线 的方程为:
的方程为: 或
或 。
。

练习册系列答案
相关题目
 ,
,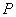 为
为 的 心.
的 心. ,当且仅当
,当且仅当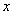 = 时,
= 时, 取到最小值为 .
取到最小值为 . 与圆
与圆 ,若在椭圆
,若在椭圆 上
上 点P,使得由点P所作的圆
点P,使得由点P所作的圆 的两条切线互相垂直,则椭圆
的两条切线互相垂直,则椭圆 B.
B. C.
C. D.
D.
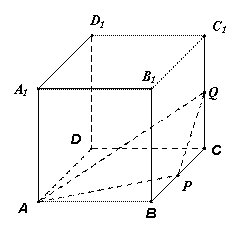
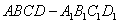 为棱长为1,动点
为棱长为1,动点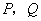 分别在棱
分别在棱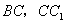 上,过点
上,过点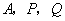 的平面截该正方体所得的截面记为
的平面截该正方体所得的截面记为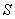 ,设
,设 其中
其中 ,下列命题正确的是
,下列命题正确的是  时,
时,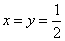 时,
时,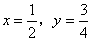 时,
时,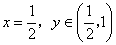 时,设
时,设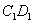 的交点为
的交点为 ,则
,则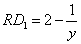
 的图象向右平移
的图象向右平移 单位后与函数
单位后与函数 的图象重合,则
的图象重合,则
 (B)
(B)
 (D)
(D)
 满足
满足 ,则
,则 的通项公式为______,若
的通项公式为______,若 ,则数列
,则数列 的前50项和为______|—
的前50项和为______|— |=1,|
|=1,| |=2,∠AOB=
|=2,∠AOB= ,
, =
=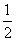

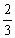 ,游览户部山、子房山和九里山的概率都是
,游览户部山、子房山和九里山的概率都是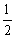 ,且该游客是否游览这四座山相互独立.
,且该游客是否游览这四座山相互独立. 山的概率;
山的概率;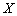 表示
表示 .
.