题目内容
数列{an}的前n项和为Sn,an是Sn和1的等差中项,等差数列{bn}满足b1+S4=0,b9=a1.
(1)求数列{an},{bn}的通项公式;
(2)若cn=
,求数列{cn}的前n项和Wn.
(1)求数列{an},{bn}的通项公式;
(2)若cn=
| 1 |
| (bn+16)(bn+18) |
考点:数列的求和,等差数列的性质
专题:计算题,等差数列与等比数列
分析:(1)由an是Sn和1的等差中项,可得Sn=2an-1,再写一式,可得数列{an}是以1为首项,2为公比的等比数列,可求数列{an}的通项公式,求出等差数列{bn}的首项与公差,可得{bn}的通项公式;
(2)利用裂项求和,可得数列{cn}的前n项和Wn.
(2)利用裂项求和,可得数列{cn}的前n项和Wn.
解答:
解:(1)∵an是Sn和1的等差中项,∴Sn=2an-1,
当n≥2时,an=Sn-Sn-1=(2an-1)-(2an-1-1)=2an-2an-1,∴an=2an-1,
当n=1时,a1=1,(2分)
∴数列{an}是以1为首项,2为公比的等比数列,
∴an=2n-1(6分)
∴Sn=2n-1;
设{bn}的公差为d,b1=-S4=-15,b9=a1=-15+8d=1,
∴d=2,
∴bn=2n-17;(8分)
(2)cn=
=
(
-
),
∴Wn=
[(1-
)+(
-
)+…+(
-
)]=
(1-
)=
-
(14分)
当n≥2时,an=Sn-Sn-1=(2an-1)-(2an-1-1)=2an-2an-1,∴an=2an-1,
当n=1时,a1=1,(2分)
∴数列{an}是以1为首项,2为公比的等比数列,
∴an=2n-1(6分)
∴Sn=2n-1;
设{bn}的公差为d,b1=-S4=-15,b9=a1=-15+8d=1,
∴d=2,
∴bn=2n-17;(8分)
(2)cn=
| 1 |
| (bn+16)(bn+18) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Wn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 4n+2 |
点评:本题考查数列的通项与求和,考查裂项法,考查学生分析解决问题的能力,难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若(2-3x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则|a0|+|a1|+|a2|+|a3|+|a4|+|a5|等于( )
| A、55 |
| B、-1 |
| C、25 |
| D、-25 |
在△ABC中,已知三边a=3,b=5,c=7,则三角形ABC是( )
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、无法确定 |
89×90×91×92×…×100可表示为( )
A、A
| ||
B、
| ||
C、
| ||
D、
|
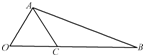 如图,∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,试求:
如图,∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,试求: