题目内容
7.正四面体ABCD的棱长为4,E为棱AB的中点,过E作此正四面体的外接球的截面,则截面面积的最小值是( )| A. | 4π | B. | 8π | C. | 12π | D. | 16π |
分析 根据题意,将四面体ABCD放置于如图所示的正方体中,则正方体的外接球就是四面体ABCD的外接球.因此利用题中数据算出外接球半径R,当球心O到截面的距离最大时,截面圆的面积达最小值,再利用球的截面圆性质可算出截面面积的最小值.
解答 解:将四面体ABCD放置于正方体中,如图所示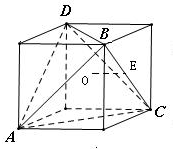
可得正方体的外接球就是四面体ABCD的外接球,
∵正四面体ABCD的棱长为4,∴正方体的棱长为2$\sqrt{2}$,
可得外接球半径R满足2R=2$\sqrt{2}$×$\sqrt{3}$,R=$\sqrt{6}$.
E为棱BC的中点,过E作其外接球的截面,当球心O到截面的距离最大时,截面圆的面积达最小值,
此时球心O到截面的距离等于正方体棱长的一半,可得截面圆的半径为r=$\sqrt{{R}^{2}-2}=2$.
得到截面圆的面积最小值为S=πr2=4π.
故选:A.
点评 本题给出正四面体的外接球,求截面圆的面积最小值.着重考查了正方体的性质、球内接多面体和球的截面圆性质等知识,属于中档题.

练习册系列答案
相关题目
18.为了解高中生对电视台某节目的态度,在某中学随机调查了110名学生,得到如下列联表:
由${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$算得${K^2}=\frac{{110×{{({40×30-20×20})}^2}}}{60×50×60×50}≈7.8$.
附表:
参照附表,得到的正确结论是( )
| 男 | 女 | 总计 | |
| 喜欢 | 40 | 20 | 60 |
| 不喜欢 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
附表:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.1%的前提下,认为“喜欢该节目与性别有关” | |
| B. | 在犯错误的概率不超过0.1%的前提下,认为“喜欢该节目与性别无关” | |
| C. | 有99%以上的把握认为“喜欢该节目与性别有关” | |
| D. | 有99%以上的把握认为“喜欢该节目与性别无关” |
15.三棱锥P-ABC的三条侧棱两两垂直,且PA=PB=PC=1,则其外接球上的点到平面ABC的距离的最大值为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{6}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
2.若如图框图所给的程序运行结果为S=41,图中的判断框①中是i>a,则实数a的取值范围是( )
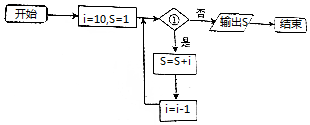

| A. | (5,6] | B. | [5,6) | C. | (6,7] | D. | [6,7) |
3.从1,2,3,4,5这五个数字中选出三个不相同数组成一个三位数,则奇数位上必须是奇数的三位数个数为( )
| A. | 12 | B. | 18 | C. | 24 | D. | 30 |