题目内容
已知△ABC的一个顶点A（3，-1），∠B被y轴平分，∠C被直线y=x平分，求直线BC的方程．
考点：直线的一般式方程
专题：直线与圆
分析：由于∠C被直线y=x平分，可得点A关于直线y=x的对称点A′（-1，3）在直线BC上；由于∠B被y轴平分，可得点A关于直线y轴的对称点A″（-3，-1）在直线BC上．
解答：
解：∵∠C被直线y=x平分，∴点A关于直线y=x的对称点A′（-1，3）在直线BC上；
∵∠B被y轴平分，∴点A关于直线y轴的对称点A″（-3，-1）在直线BC上．
∴直线BC的方程为：y-3=
(x+1)，
化为2x-y+5=0．
∵∠B被y轴平分，∴点A关于直线y轴的对称点A″（-3，-1）在直线BC上．
∴直线BC的方程为：y-3=
| -1-3 |
| -3-(-1) |
化为2x-y+5=0．
点评：本题考查了角平分线的性质、轴对称、直线的方程，属于基础题．
练习册系列答案
优学名师名题系列答案
相关题目
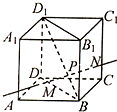正方体ABCD-A1B1C1D1，P在BD1上，过P作垂直于BD1的平面α，记这样得到的截面多边形（含三角形）周长为y，为什么当α在平面AB1C，面A1DC1之间运动时，y不变？