题目内容

19．若x，y满足$\left\{\begin{array}{l}{x-y≥1}\\{x+y≤4}\\{x≥0}\\{y≥0}\end{array}\right.$，则z=x-2y的最大值是（　　）
A．-$\frac{1}{2}$B．1C．2D．4

分析 画出不等式组表示的平面区域，结合图形知函数z=x-2y取得最大值时对应点的坐标，从而求出最大值．

解答 解：画出不等式组$\left\{\begin{array}{l}{x-y≥1}\\{x+y≤4}\\{x≥0}\\{y≥0}\end{array}\right.$表示的平面区域，如图所示；

由$\left\{\begin{array}{l}{x+y=4}\\{y=0}\end{array}\right.$解得点B（4，0），
此时函数z=x-2y取得最大值为zmax=4-2×0=4．
故选：D．

点评 本题考查了线性规划的应用问题，是基础题．

练习册系列答案
相关题目
2．已知数列{an}的前n项和Sn满足Sn=$\frac{3}{2}$n2+$\frac{7}{2}$n（n∈N*），数列{bn}是首项为4的正项等比数列，且2b2，b3-3，b2+2成等差数列．
（Ⅰ）求数列{an}，{bn}的通项公式；
（Ⅱ）令cn=an•bn（n∈N*），求数列{cn}的前n项和Tn．
10．已知直线l的参数方程$\left\{\begin{array}{l}{x=t}\\{y=1+2t}\end{array}\right.$（t为参数），若以原点O为极点，x轴的正半轴为极轴，建立极坐标系，圆C的极坐标方程为ρ=2$\sqrt{2}$sin（θ+$\frac{π}{4}$）．则圆的直角坐标方程为（x-1）2+（y-1）2=2，直线l和圆C的位置关系为相交（填相交、相切、相离）．
7．在直角坐标系xOy中，直线${C_1}：y=\sqrt{3}x$，曲线C2的参数方程是$\left\{\begin{array}{l}x=\sqrt{3}+cosθ\\ y=-2+sinθ\end{array}\right.$（θ为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．
（1）求C1的极坐标方程和C2的普通方程；
（2）把C1绕坐标原点沿逆时针方向旋转$\frac{π}{3}$得到直线C3，C3与C2交于A，B两点，求|AB|．
14．给出下列四个结论：
（1）如果${（3x-\frac{1}{{\root{3}{x^2}}}）^n}$的展开式中各项系数之和为128，则展开式中$\frac{1}{x^3}$的系数是-21；
（2）用相关指数r来刻画回归效果，r的值越大，说明模型的拟合效果越差；
（3）若f（x）是R上的奇函数，且满足f（x+2）=-f（x），则f（x）的图象关于x=1对称；
（4）一个篮球运动员投篮一次得3分的概率为a，得2分的概率为b，不得分的概率为c，且a，b，c∈（0，1），已知他投篮一次得分的数学期望为2，则$\frac{2}{a}+\frac{1}{3b}$的最小值为$\frac{16}{3}$；
其中正确结论的序号为（3）（4）．
4．在极坐标系中，过点（1，0）并且与极轴垂直的直线方程是（　　）
A．ρcosθ=1B．ρsinθ=1C．ρ=cosθD．ρ=sinθ
11．如图，在三棱柱ABC-A1B1C1中，面ABB1A1为矩形，AB=1，AA1=$\sqrt{2}$，D为AA1的中点，BD与AB1交于点O，CO⊥面ABB1A1
（Ⅰ）证明：BC⊥AB1
（Ⅱ）若OC=OA，求二面角A-BC-B1的余弦值．
8．已知函数y=x2的图象在点（x0，x02）处的切线为直线l，若直线l与函数y=lnx（x∈（0，1））的图象相切，则满足（　　）
A．x0∈（$\sqrt{2}$，$\sqrt{3}$）B．x0∈（1，$\sqrt{2}$）C．x0∈（0，$\frac{1}{2}$）D．x0∈（$\frac{1}{2}$，1）
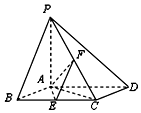9．如图所示，已知四棱锥P-ABCD中，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E，F分别是线段BC，PC的中点
（1）证明：AE⊥PD
（2）若H为PD上的动点，EH与平面PAD所成最大角的正切值为$\sqrt{3}$，求二面角E-AF-C的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网