题目内容
9.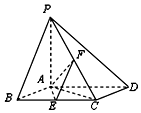 如图所示,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是线段BC,PC的中点
如图所示,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是线段BC,PC的中点(1)证明:AE⊥PD
(2)若H为PD上的动点,EH与平面PAD所成最大角的正切值为$\sqrt{3}$,求二面角E-AF-C的余弦值.
分析 (1)推导出△ABC为正三角形,从而AE⊥AD,由PA⊥平面ABCD,得PA⊥AE,从而AE⊥平面PAD,由此能证明AE⊥PD.
(2)设AB=2,H为PD上任意一点,连接AH,EH,由AE⊥平面PAD,知∠EHA为EH与平面PAD所成的角,当AH最短即AH⊥PD时,∠EHA最大,由AE,AD,AP两两互相垂直,以A为坐标原点,建立空间直角坐标系A-xyz,利用向量法能求出二面角E-AF-C的余弦值.
解答 证明:(1)∵四边形ABCD是菱形,∠ABC=60°,∴△ABC为正三角形
∵E为BC的中点,∴AE⊥BC,又∵BC∥AD,∴AE⊥AD
∵PA⊥平面ABCD,AE?平面ABCD,∴PA⊥AE
∵PA?平面PAD,AD?平面PAD,且PA∩AD=A,
∴AE⊥平面PAD,∵PD?平面PAD,∴AE⊥PD.…(4分)
解:(2)设AB=2,H为PD上任意一点,连接AH,EH,
由(1)知AE⊥平面PAD,则∠EHA为EH与平面PAD所成的角.
在Rt△EAH中,AE=$\sqrt{3}$,∴当AH最短即AH⊥PD时,∠EHA最大.
此时tan∠EHA=$\frac{AE}{AH}=\frac{{\sqrt{3}}}{AH}=\sqrt{3}$,∴AH=1
又∵AD=2,∴∠ADH=30°
∴PA=ADtan30°=$\frac{{2\sqrt{3}}}{3}$…(6分)
由(1)知AE,AD,AP两两互相垂直,以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,
又∵E,F分别为BC,PC的中点,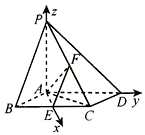
∴A(0,0,0),B($\sqrt{3}$,-1,0),C($\sqrt{3}$,1,0),D(0,2,0),P(0,0,$\frac{{2\sqrt{3}}}{3}$),E($\sqrt{3}$,0,0),F($\frac{{\sqrt{3}}}{2}$,$\frac{1}{2}$,$\frac{{\sqrt{3}}}{3}$)
∴$\overrightarrow{AE}=(\sqrt{3},0,0)$,$\overrightarrow{AF}=(\frac{{\sqrt{3}}}{2},\frac{1}{2},\frac{{\sqrt{3}}}{3})$,$\overrightarrow{BD}=(-\sqrt{3},3,0)$
设平面AEF的法向量m=(x1,y1,z1)
则$\left\{\begin{array}{l}m•\overrightarrow{AE}=0\\ m•\overrightarrow{AF}=0\end{array}\right.$,即$\left\{\begin{array}{l}\sqrt{3}{x_1}=0\\ \frac{{\sqrt{3}}}{2}{x_1}+\frac{1}{2}{y_1}+\frac{{\sqrt{3}}}{3}{z_1}=0\end{array}\right.$
取z1=-1,则m=$({0,\frac{{2\sqrt{3}}}{3},-1})$
∵BD⊥AC,BD⊥PA,PA∩AC=A,∴BD⊥平面AFC
∴平面AFC的一个法向量为$\overrightarrow{BD}=(-\sqrt{3},3,0)$
∴cos<m,$\overrightarrow{BD}$>=$\frac{{m•\overrightarrow{BD}}}{{|m|•|{\overrightarrow{BD}}|}}=\frac{{2\sqrt{3}}}{{\sqrt{\frac{7}{3}}×\sqrt{12}}}=\frac{{\sqrt{21}}}{7}$…(11分)
∵二面角E-AF-C为锐二面角,∴所求二面角的余弦值为$\frac{{\sqrt{21}}}{7}$…(12分)
点评 本题考查线线垂直的证明,考查二面角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

 ABC考王全优卷系列答案
ABC考王全优卷系列答案| A. | -$\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | b<a<c |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{5}$ |
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
| A. | $\frac{5}{7}$ | B. | $\frac{7}{9}$ | C. | $\frac{10}{11}$ | D. | $\frac{11}{23}$ |



