题目内容
(2012•桂林模拟)设a∈R,函数f(x)=ex+a•e﹣x的导函数是f′(x),且f′(x)是奇函数.若曲线y=f(x)的一条切线的斜率是 ,则切点的横坐标为( )
,则切点的横坐标为( )
A.ln2 B.﹣ln2 C.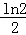 D.
D.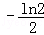
A
【解析】
试题分析:已知切线的斜率,要求切点的横坐标必须先求出切线的方程,
我们可从奇函数入手求出切线的方程.
【解析】
对f(x)=ex+a•e﹣x求导得
f′(x)=ex﹣ae﹣x
又f′(x)是奇函数,故
f′(0)=1﹣a=0
解得a=1,故有
f′(x)=ex﹣e﹣x,
设切点为(x0,y0),则
 ,
,
得 或
或 (舍去),
(舍去),
得x0=ln2.

练习册系列答案
相关题目

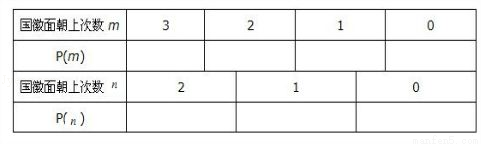
 (a>0,且a≠1),f′(x)g(x)<f(x)g′(x),
(a>0,且a≠1),f′(x)g(x)<f(x)g′(x), ,则a的值为( )
,则a的值为( ) C.
C. D.
D.
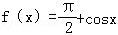 ,则f′(
,则f′(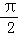 )=( )
)=( ) ex(sinx+cosx)在区间[0,
ex(sinx+cosx)在区间[0, ]上的值域为( )
]上的值域为( ) e
e ] B.(
] B.(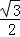 B.
B.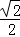 C.
C.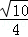 D.
D.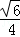
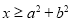 ,则
,则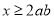 ”的逆命题是
”的逆命题是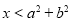 ,则
,则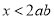
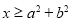 ,则
,则