题目内容
如图,一个底面半径为R的圆柱被与其底面所成角为θ(0°<θ<90°)的平面所截,截面是一个椭圆,
当θ为30°时,这个椭圆的离心率为 .


【解析】
试题分析:利用已知条件,求出题意的长半轴,短半轴,然后求出半焦距,即可求出题意的离心率.
【解析】
因为底面半径为R的圆柱被与底面成30°的平面所截,其截口是一个椭圆,
则这个椭圆的短半轴为:R,长半轴为: ,
,
∵a2=b2+c2,∴c= ,
,
∴椭圆的离心率为:e= =
= .
.
故答案为: .
.

练习册系列答案
相关题目
 有两项
有两项 和
和 ,满足
,满足 ,则该数列前
,则该数列前 项之和为 ( )
项之和为 ( ) B
B  C
C  D
D 
 ,则输入的
,则输入的 可能为
可能为
 B.
B. C.
C. D.
D.
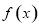 是定义域为正整数集的函数,具有如下性质:对于定义域内任意的
是定义域为正整数集的函数,具有如下性质:对于定义域内任意的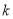 ,如果
,如果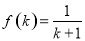 成立,则
成立,则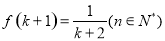 成立,那么下列命题正确的是___
成立,那么下列命题正确的是___ 成立,则对于任意
成立,则对于任意 ,均有
,均有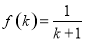
 成立,则对于任意
成立,则对于任意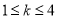 ,均有
,均有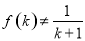
 成立,则对于任意
成立,则对于任意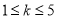 ,均有
,均有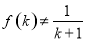
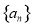 的首项
的首项 ,公比为
,公比为 ,前
,前 项和为
项和为 ,若
,若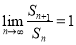 ,则公比为
,则公比为 的取值范围是_____________.
的取值范围是_____________.
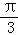 ,点A与B、C两点间的球面距离均为
,点A与B、C两点间的球面距离均为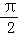 ,O为球心,
,O为球心,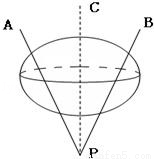
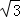 B.
B. C.2 D.
C.2 D.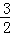
 ,则切点的横坐标为( )
,则切点的横坐标为( )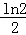 D.
D.