题目内容
函数f（x）=
（x∈R）（ ）
| 4x |
| x2+1 |
| A、既有最大值2，又有最小值-2 |
| B、无最大值，但有最小值-2 |
| C、有最大值2，但无最小值 |
| D、既无最大值，又无最小值 |
考点：利用导数研究函数的极值
专题：导数的概念及应用
分析：先求出函数的导数，找到单调区间，从而求出最大值和最小值．
解答：
解：f′(x)=
=
，
令f'（x）=0，得x=±1．
x，f′（x），f（x）的变化如下表：
∴f（x）在（-∞，-1），（1，+∞）上递减，在（-1，1）上递增，
∴f（x）极小值=f（-1）=-2，f（x）极大值=f（1）=2，
又当x→∞时，f（x）→0，
故选A．
| 4(x2+1)-4x•2x |
| (x2+1)2 |
| 4-4x2 |
| (x2+1)2 |
令f'（x）=0，得x=±1．
x，f′（x），f（x）的变化如下表：
| x | （-∞，-1） | -1 | （-1，1） | 1 | （1，+∞） |
| f'（x） | - | 0 | + | 0 | - |
| f（x） | ↘ | 极小值-2 | ↗ | 极大值2 | ↘ |
∴f（x）极小值=f（-1）=-2，f（x）极大值=f（1）=2，
又当x→∞时，f（x）→0，
故选A．
点评：本题考察了函数的单调性，函数的最值问题，导数的应用，是一道基础题．
练习册系列答案
相关题目
定义在复数集上的函数f（z-i）=
，则f（i）=（ ）
| ||
| 1-z |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
已知命题“p：x≥4或x≤0”，命题“q：x∈Z”，如果“p且q”与“非q”同时为假命题，则满足条件的x为（ ）
| A、{x|x≥3或x≤-1，x∉Z} |
| B、{x|-1≤x≤3，x∉Z} |
| C、{-1，0，1，2，3} |
| D、{1，2，3} |
某程序框图如图所示，当a=3时，此程序输出的结果是（ ）
| A、9 | B、3 | C、10 | D、6 |
对于非零向量
、
，下列命题中正确的是（ ）
| a |
| b |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
在区间[0，2]和[1，2]上分别取一个数x，y，则对应的数对（x，y）是不等式x-y≤0的解的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f（x）=
，类比课本推导等差数列前n项和公式的推导方法计算f（-4）+f（-3）+…+f（0）+f（1）+…+f（4）+f（5）的值为（ ）
| 1 | ||
2x+
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
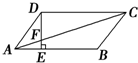如图所示，在平行四边形ABCD中，AE：EB=1：2，若S△AEF=6cm2，则S△ADF为（ ）| A、54cm2 |
| B、24cm2 |
| C、18cm2 |
| D、12cm2 |