题目内容
15.f(x)=ex-ax+1在R上不是单调函数的充要条件是a>0.分析 f(x)=ex-ax+1在R上不是单调函数的充要条件是f′(x)=0在R上有解,即可得出.
解答 解:f′(x)=ex-a,
f(x)=ex-ax+1在R上不是单调函数的充要条件是f′(x)=0在R上有解,
∴a=ex>0.
故答案为:a>0.
点评 本题考查了利用导数研究函数的单调性极值、方程的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.一个圆过点(-5,1)且圆心在直线2x+y+4=0上,求半径最小时的圆心坐标( )
| A. | (-1,-2) | B. | (-2,0) | C. | (-$\frac{5}{2}$,1) | D. | (-3,2) |
6.已知函数f(x)=ex-ax-1,g(x)=ln(ex-1)-lnx,若?x0∈(0,+∞),使得f(g(x0)>f(x0)成立,则a的取值范围是( )
| A. | (0,+∞) | B. | (0,1) | C. | (1,+∞) | D. | [1,+∞) |
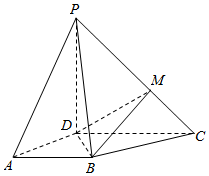 如图,四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,∠BAD=$\frac{π}{3}$,AB=2,CD=3,M为PC上一点,PM=2MC.
如图,四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,∠BAD=$\frac{π}{3}$,AB=2,CD=3,M为PC上一点,PM=2MC.