题目内容
化简
= (
<θ<2π).
|
| 3π |
| 2 |
考点:三角函数的恒等变换及化简求值
专题:计算题
分析:(1)利用二倍角余弦公式的变形进行转化去根号是解决本题的关键,即将被开方数进行升幂转化,结合角所在的象限进行开方化简.
解答:
解:
=
=
=|cos
|,
由于
<θ<2π,则
<
<π,
故cos
<0,因此原式化简之后得到-cos
.
故答案为:-cos
.
|
|
|
| θ |
| 2 |
由于
| 3π |
| 2 |
| 3π |
| 4 |
| θ |
| 2 |
故cos
| θ |
| 2 |
| θ |
| 2 |
故答案为:-cos
| θ |
| 2 |
点评:本题考查三角函数的恒等变换,考查基本的三角变换公式的运用,主要考查二倍角余弦公式的变形公式的运用,考查带根号问题的处理方法,考查学生的转化与化归思想和方法,注意角所在象限对三角函数正负的影响.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
方程组
共有( )组解.
|
| A、1 | B、2 | C、3 | D、4 |
空间四个不同的平面,它们有多种位置关系,从交线数目看,所有可能出现的交线数目的集合是( )
| A、{0,1,2,3,4,5,6} |
| B、{0,1,3,4,5,6} |
| C、{0,1,2,3,5,6} |
| D、{0,1,3,4} |
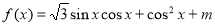 ,
,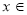
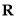 .
. 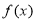 的最小正周期及单调递增区间;
的最小正周期及单调递增区间; 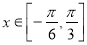 时,
时,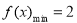 ,求函数
,求函数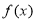 的最大值,并指出
的最大值,并指出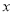 取何值时,函数
取何值时,函数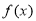 取得最大值.
取得最大值.