题目内容
函数y=2cosx(sinx-cosx),x∈[
,
]的值域是 .
| π |
| 8 |
| 3π |
| 4 |
考点:三角函数中的恒等变换应用
专题:三角函数的求值
分析:由三角函数公式化简可得y=
sin(2x-
)-1,由x∈[
,
]和三角函数的性质逐步求范围可得.
| 2 |
| π |
| 4 |
| π |
| 8 |
| 3π |
| 4 |
解答:
解:化简可得y=2cosx(sinx-cosx)
=2sinxcosx-2cos2x=sin2x-cos2x-1
=
sin(2x-
)-1,
∵x∈[
,
],∴2x-
∈[0,
],
∴sin(2x-
)∈[-
,1],
∴
sin(2x-
)-1∈[-2,
-1],
故答案为:[-2,
-1],
=2sinxcosx-2cos2x=sin2x-cos2x-1
=
| 2 |
| π |
| 4 |
∵x∈[
| π |
| 8 |
| 3π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
∴sin(2x-
| π |
| 4 |
| ||
| 2 |
∴
| 2 |
| π |
| 4 |
| 2 |
故答案为:[-2,
| 2 |
点评:本题考查三角函数的值域,涉及三角函数的化简,属基础题.

练习册系列答案
相关题目
设
,
是两个不共线的向量,若向量
=-
+k
(k∈R)与向量
=
-2
共线,则( )
| e1 |
| e2 |
| m |
| e1 |
| e2 |
| n |
| e2 |
| e1 |
| A、k=0 | B、k=1 |
| C、k=2 | D、k=0.5 |
已知sinα-cosα=
,则tanα+
=( )
| 1 |
| 3 |
| 1 |
| tanα |
A、
| ||
B、
| ||
C、
| ||
D、
|
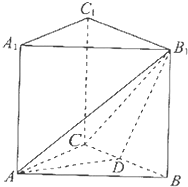 如图,在棱长均相等的正三棱柱ABC-A1B1C1中,D为BC的中点.
如图,在棱长均相等的正三棱柱ABC-A1B1C1中,D为BC的中点.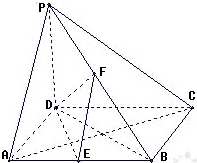 已知四棱锥P-ABCD,底面是边长为a的正方形,PD⊥底面ABCD,PD=DC,E、F分别是AB、PB的中点,
已知四棱锥P-ABCD,底面是边长为a的正方形,PD⊥底面ABCD,PD=DC,E、F分别是AB、PB的中点,