题目内容
2.已知P(-2,-3)和以Q为圆心的圆(x-4)2+(y-2)2=9.(1)求出以PQ为直径的圆Q1的一般式方程.
(2)若圆Q和圆Q1交于A、B两点,直线PA、PB是以Q为圆心的圆的切线吗?为什么?
(3)求直线AB的方程.
分析 (1)由圆(x-4)2+(y-2)2=9可得圆心Q(4,2).线段PQ的中点Q1(1,-$\frac{1}{2}$),|PQ1|=$\frac{\sqrt{61}}{2}$,即可得出.
(2)由于∠PAQ是以PQ为直径的圆周角,可得∠PAQ=90°.因此直线PA是以Q为圆心的圆的切线.同理PB是以Q为圆心的圆的切线.
(3)由于交点A,B既在圆(x-4)2+(y-2)2=9上,又在圆(x-1)2+(y+$\frac{1}{2}$)2=$\frac{61}{4}$上.两方程相减即可得出直线AB的方程.
解答 解:(1)由圆(x-4)2+(y-2)2=9可得圆心Q(4,2).
∴线段PQ的中点Q1(1,-$\frac{1}{2}$),|PQ1|=$\frac{\sqrt{61}}{2}$.
∴以PQ为直径,Q1为圆心的圆的方程为(x-1)2+(y+$\frac{1}{2}$)2=$\frac{61}{4}$;
(2)∵∠PAQ是以PQ为直径的圆周角,∴∠PAQ=90°.
∴直线PA是以Q为圆心的圆的切线.
同理PB是以Q为圆心的圆的切线.
(3)由于交点A,B既在圆(x-4)2+(y-2)2=9上,又在圆(x-1)2+(y+$\frac{1}{2}$)2=$\frac{61}{4}$上.
两方程相减可得:6x+5y=25,即为直线AB的方程.
点评 本题考查了圆的标准方程及其性质、圆的切线的性质、两圆相交的性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
16.已知A={x|$\frac{6}{x+2}$>1},B={x|x-a<0}.
(1)若A∩B=(-2,0),求a的取值范围;
(2)若A∩B=∅,求a的取值范围;
(3)若A∩B=A,求a的取值范围.
(1)若A∩B=(-2,0),求a的取值范围;
(2)若A∩B=∅,求a的取值范围;
(3)若A∩B=A,求a的取值范围.
14.若直线(a+1)x+2y=2与直线x+ay=1互相平行,则实数a的值等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | -2 |
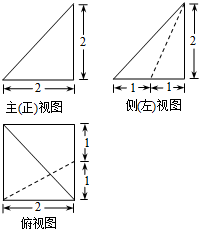 已知四棱锥的三视图(如图所示),则该四棱锥的体积为2,在该四棱锥的四个侧面中,面积最小的侧面面积是1.
已知四棱锥的三视图(如图所示),则该四棱锥的体积为2,在该四棱锥的四个侧面中,面积最小的侧面面积是1.