题目内容
11．
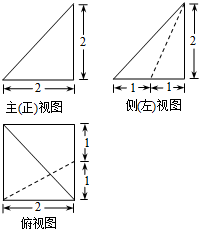已知四棱锥的三视图（如图所示），则该四棱锥的体积为2，在该四棱锥的四个侧面中，面积最小的侧面面积是1．
分析 画出图形，利用三视图的数据，求解棱锥的体积及面积最小的侧面面积即可．
解答 解：由题意可知几何体为如图所示的四棱锥：
棱锥的底面是下底为2，高为2，上底为1的梯形，棱锥的高为2，
四棱锥的体积为：$\frac{1}{3}$×2×$\frac{1}{2}$×（1+2）×2=2．
面积最小的侧面面积是：$\frac{1}{2}×1×2$=1．
故答案为：2，1．
点评 本题考查三视图与几何体是直观图的关系，几何体的体积的求法，考查计算能力．解决此类问题的关键是根据三视图正确还原几何体．
练习册系列答案
相关题目
16．函数f（x）的定义域为D，对给定的正数k，若存在闭区间[a，b]⊆D，使得函数f（x）满足：①f（x）在[a，b]内是单调递增函数；②f（x）在[a，b]上的值域为[ka，kb]，则称区间[a，b]为y=f（x）的k级“调和区间”．下列结论错误的是（ ）
| A． | 函数f（x）=x3（x∈[-2016，2016]存在1级“调和区间” | |
| B． | 函数f（x）=ex（x∈R）不存在2级“调和区间” | |
| C． | 函数f（x）=5elnx存在3级“调和区间” | |
| D． | 函数f（x）=tanx（x$∈（-\frac{π}{2}，\frac{π}{2}）$）不存在4级“调和区间” |